《2025年新课标学习方法指导丛书八年级数学上册浙教版》

1. 已知等腰三角形有一个角是 $90^\circ$,则另两个角分别是(B)
A.$30^\circ,60^\circ$
B.$45^\circ,45^\circ$
C.$45^\circ,90^\circ$
D.$20^\circ,70^\circ$

答案： B

2. 已知等腰三角形的顶角是 $80^\circ$,则一腰上的高与底边的夹角是(A)
A.$40^\circ$
B.$50^\circ$
C.$60^\circ$
D.$30^\circ$

答案： A

3. 如图,在$\triangle ABC$中,$AC= BC$,点 D 在 BC 的延长线上,$AE// BD$,点 E,D 在 AC 同侧,若$\angle CAE= 118^\circ$,则$\angle B$的度数为(A)
A.$31^\circ$
B.$32^\circ$
C.$59^\circ$
D.$62^\circ$

答案： A

4. 如图,在$\triangle ABC$中,$AB= AC$,$\angle A= 30^\circ$,E 为 BC 延长线上一点,$\angle ABC与\angle ACE$的平分线相交于点 D,则$\angle D$的度数为(A)

A.$15^\circ$
B.$17.5^\circ$
C.$20^\circ$
D.$22.5^\circ$

答案： A

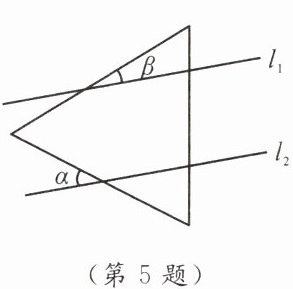
5. 已知直线$l_{1}// l_{2}$,将等边三角形如图放置,若$\angle \alpha =40^\circ$,则$\angle \beta=$20°。

答案： 20

6. 已知一个等腰三角形,其中一条腰上的高与另一条腰的夹角为$25^\circ$,则该等腰三角形的顶角为______65°或115°。

答案： 由于题目要求填写答案格式，这里应列出两个可能的答案格式，但按常规选择题设定，我们假设题目已设定两个选项对应这两个答案，此处直接给出计算结果：
答案填：65°或115°（若为选择题则根据选项填对应字母）

7. 如图,在等边$\triangle ABC$中,$AC\perp CD$,垂足为 C,$BC= CD$,求$\angle ABD$的度数。

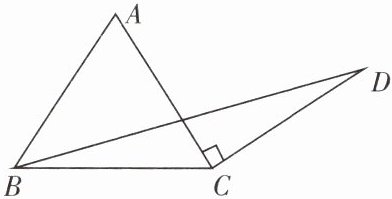
答案： $\because\triangle ABC$是等边三角形，
$\therefore\angle ABC=\angle ACB=60^{\circ}$。
$\because AC\perp CD$，
$\therefore\angle ACD=90^{\circ}$。
$\therefore\angle BCD=\angle ACB+\angle ACD=150^{\circ}$。
$\because BC=CD$，
$\therefore\angle CBD=\angle CDB=\frac{180^{\circ}-\angle BCD}{2}=15^{\circ}$。
$\therefore\angle ABD=\angle ABC-\angle CBD=60^{\circ}-15^{\circ}=45^{\circ}$。