《2025年新课标学习方法指导丛书八年级数学上册浙教版》

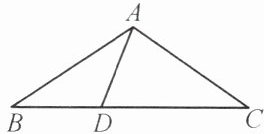
8. 如图所示,D 是$\triangle ABC$的边 BC 上的一点,且$DA= DB$,$AB= AC= CD$,求$\angle CAD$的大小。

答案： 设∠B=∠C=x。
∵AB=AC，
∴∠B=∠C=x（等腰三角形两底角相等）。
∵DA=DB，
∴∠DAB=∠B=x（等腰三角形两底角相等）。
在△ABD中，∠ADB=180°-∠DAB-∠B=180°-2x（三角形内角和定理）。
∵∠ADB+∠ADC=180°（平角定义），
∴∠ADC=180°-∠ADB=2x。
∵AC=CD，
∴∠CAD=∠ADC=2x（等腰三角形两底角相等）。
在△ABC中，∠BAC=∠BAD+∠CAD=x+2x=3x。
∵∠B+∠C+∠BAC=180°（三角形内角和定理），
∴x+x+3x=180°，解得x=36°。
∴∠CAD=2x=72°。
72°

9. 如图,$AB= AC= AD$,若$\angle BAD= 80^\circ$,则$\angle BCD$的度数为(C)
A.$80^\circ$
B.$100^\circ$
C.$140^\circ$
D.$160^\circ$

答案： C

10. 如图,在$\triangle ABC$中,$AB= AC$,$AE= AF= BE$,$\angle BAE= 40^\circ$,则$\angle FEC$的度数为(C)
A.$10^\circ$
B.$15^\circ$
C.$20^\circ$
D.$25^\circ$

答案： C

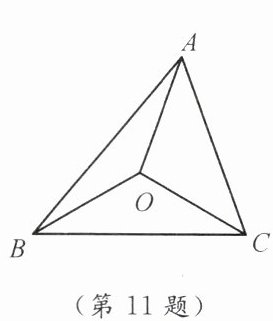
11. 如图,O 为$\triangle ABC$内一点,且$OA= OB= OC$,$\angle ABO= 20^\circ$,$\angle BCO= 30^\circ$,则$\angle CAO= $40°。

答案： 40

12. 如图,在等边三角形 ABC 中,点 D,E 分别在边 AB,BC 上,把$\triangle BDE$沿直线 DE 翻折,使点 B 落在点$B'$处,$DB'$,$EB'$分别交 AC 于点 F,G。若$\angle ADF= 70^\circ$,则$\angle BED= $65°。

答案： 65

13. 如图,在$\triangle ABC$中,$AB= AC$,$\angle A= 36^\circ$,AC 的垂直平分线交 AB 于点 E,D 为垂足,连结 EC,求$\angle ECB$的度数。

答案：
∵AB=AC，∠A=36°，
∴∠B=∠ACB=(180°-36°)/2=72°。
∵ED是AC的垂直平分线，
∴EA=EC，
∴∠ECA=∠A=36°，
∴∠ECB=∠ACB - ∠ECA=72°-36°=36°。
答：∠ECB的度数为36°。