第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
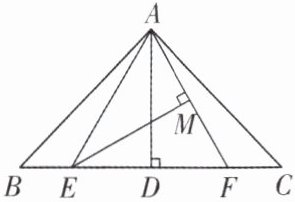
例3 如图,在△ABC中,AB = AC,且AD⊥BC,在线段BC上取E,F两点,使BE = CF,连接AE,AF.
(1)求证:AD平分∠EAF;
(2)过点E作EM⊥AF于点M,若DE = MF,求证:△AEF是等边三角形.
(1)求证:AD平分∠EAF;
(2)过点E作EM⊥AF于点M,若DE = MF,求证:△AEF是等边三角形.

答案:
(1)证明:
∵AB=AC,AD⊥BC,
∴BD=CD(等腰三角形三线合一)。
∵BE=CF,
∴BD-BE=CD-CF,即DE=DF。
在△ADE和△ADF中,
$\left\{\begin{array}{l} AD=AD\\ ∠ADE=∠ADF=90°\\ DE=DF\end{array}\right.$,
∴△ADE≌△ADF(SAS),
∴∠EAD=∠FAD,即AD平分∠EAF。
(2)证明:由
(1)知△ADE≌△ADF,
∴AE=AF,DE=DF。
∵EM⊥AF,AD⊥BC,
∴∠EMF=∠ADF=90°。
又∠EFM=∠AFD(公共角),MF=DE=DF,
在△EMF和△ADF中,
$\left\{\begin{array}{l} ∠EMF=∠ADF\\ ∠EFM=∠AFD\\ MF=DF\end{array}\right.$,
∴△EMF≌△ADF(AAS),
∴EF=AF。
∵AE=AF,
∴AE=AF=EF,故△AEF是等边三角形。
(1)证明:
∵AB=AC,AD⊥BC,
∴BD=CD(等腰三角形三线合一)。
∵BE=CF,
∴BD-BE=CD-CF,即DE=DF。
在△ADE和△ADF中,
$\left\{\begin{array}{l} AD=AD\\ ∠ADE=∠ADF=90°\\ DE=DF\end{array}\right.$,
∴△ADE≌△ADF(SAS),
∴∠EAD=∠FAD,即AD平分∠EAF。
(2)证明:由
(1)知△ADE≌△ADF,
∴AE=AF,DE=DF。
∵EM⊥AF,AD⊥BC,
∴∠EMF=∠ADF=90°。
又∠EFM=∠AFD(公共角),MF=DE=DF,
在△EMF和△ADF中,
$\left\{\begin{array}{l} ∠EMF=∠ADF\\ ∠EFM=∠AFD\\ MF=DF\end{array}\right.$,
∴△EMF≌△ADF(AAS),
∴EF=AF。
∵AE=AF,
∴AE=AF=EF,故△AEF是等边三角形。
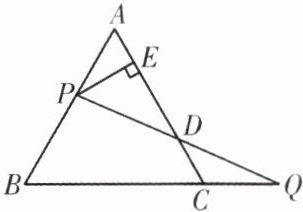
巩固提升 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,连接PQ交AC边于D,当PA = CQ时,DE的长为
$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
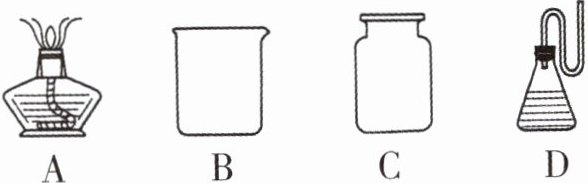
1. (2024·重庆A)下列四种化学仪器的示意图中,是轴对称图形的是(
C
)
答案:
C
2. 生物小组的同学想用18米长的篱笆围一个等腰三角形区域作为苗圃,如果苗圃的一边长是4米,那么苗圃的另外两边长分别是(
A.4米、4米
B.4米、10米
C.7米、7米
D.7米、7米,或4米、10米
C
)A.4米、4米
B.4米、10米
C.7米、7米
D.7米、7米,或4米、10米
答案:
C
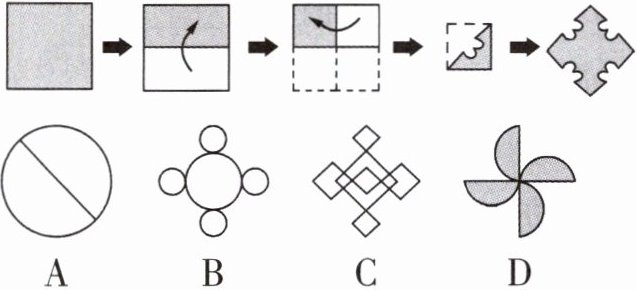
3. 剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(先将纸折叠,然后剪纸,展开即得到图案),则下列四个图案,不能用上述方法剪出的是(
D
)
答案:
D
4. 如图是某学校人行人口的智能闸机及其示意图.当它关闭时,双侧挡板边缘的端点A与B之间的距离为10cm,挡板边缘AC = BD = 70cm,且与闸机侧立面的夹角∠ACP = ∠BDQ = 30°.当挡板收起后,可以通过闸机的物体的最大宽度为(
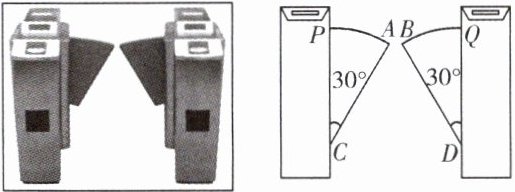
A.(70√2 + 10)cm
B.80cm
C.(70√3 + 10)cm
D.90cm
B
)
A.(70√2 + 10)cm
B.80cm
C.(70√3 + 10)cm
D.90cm
答案:
B
5. 数学知识的呈现一般表现出连贯性、一致性,所以在学习数学知识的过程中应该学会将新知识纳入已学的知识框架内,形成知识体系.小加在复习三角形时将几种三角形的关系整理如下图.请帮他在括号内填上一个适当的条件
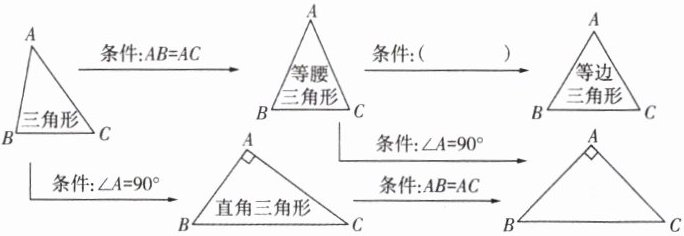
∠A=60°(或∠B=60°或∠C=60°)
.
答案:
∠A=60°(或∠B=60°或∠C=60°)
查看更多完整答案,请扫码查看


