第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
变式训练 三角形按角分类可以分为(
A. 锐角三角形、直角三角形、钝角三角形
B. 等腰三角形、等边三角形、不等边三角形
C. 直角三角形、等腰直角三角形
D. 以上答案都不正确
A
)A. 锐角三角形、直角三角形、钝角三角形
B. 等腰三角形、等边三角形、不等边三角形
C. 直角三角形、等腰直角三角形
D. 以上答案都不正确
答案:
A
1. 下面是小强用三根火柴组成的图形,其中符合三角形概念的是(

C
)
答案:
C
2. 三角形按边的相等关系分类用如图所示的集合来表示,则图中 $M$,$N$ 分别表示的三角形是(
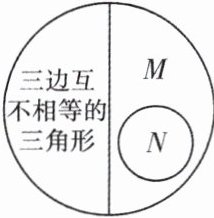
A.等边三角形、等腰三角形
B.等腰三角形、等边三角形
C.锐角三角形、等腰三角形
D.等腰三角形、锐角三角形
B
)
A.等边三角形、等腰三角形
B.等腰三角形、等边三角形
C.锐角三角形、等腰三角形
D.等腰三角形、锐角三角形
答案:
B
3. 下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是(

B
)
答案:
B
4. 如图,点 $B$ 是射线 $AM$ 上一点,且 $\angle A = 40^{\circ}$,给出两个结论:
结论Ⅰ:若 $\triangle ABC$ 是直角三角形,则有 $\angle C = 90^{\circ}$.
结论Ⅱ:若 $\triangle ABC$ 是钝角三角形,则有 $90^{\circ} \lt \angle C \lt 180^{\circ}$.
下列说法正确的是(

A.结论Ⅰ和结论Ⅱ都正确
B.结论Ⅰ和结论Ⅱ都不正确
C.只有结论Ⅰ正确
D.只有结论Ⅱ正确
结论Ⅰ:若 $\triangle ABC$ 是直角三角形,则有 $\angle C = 90^{\circ}$.
结论Ⅱ:若 $\triangle ABC$ 是钝角三角形,则有 $90^{\circ} \lt \angle C \lt 180^{\circ}$.
下列说法正确的是(
B
)
A.结论Ⅰ和结论Ⅱ都正确
B.结论Ⅰ和结论Ⅱ都不正确
C.只有结论Ⅰ正确
D.只有结论Ⅱ正确
答案:
B
5. 在平面内,分别用长度相同的 $3$ 根、$5$ 根、$6$ 根火柴首尾顺次相接,能搭成什么形状的三角形呢?通过尝试,列表如下:
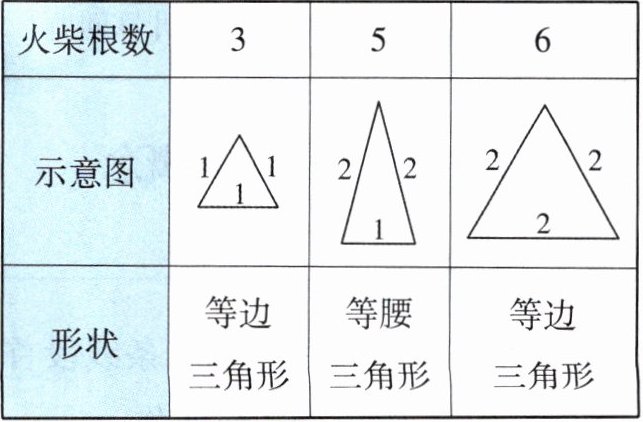
(1) $4$ 根火柴能搭成三角形吗?
(2) $12$ 根火柴能搭成等腰三角形吗?能搭成等边三角形吗?若能,请画出示意图.

(1) $4$ 根火柴能搭成三角形吗?
(2) $12$ 根火柴能搭成等腰三角形吗?能搭成等边三角形吗?若能,请画出示意图.
答案:
(1) 不能;
(2) 能搭成等腰三角形:
设等腰三角形腰长为$x$根火柴,底长为$y$根火柴,
则$2x + y = 12$,
根据三角形三边关系$2x>y$且$|x - x|<y$(显然成立),
由$2x + y = 12$和$2x>y$,可得$12 - y>y$,$y < 6$,
同时$y>0$,且$x=\frac{12 - y}{2}$为正整数,
当$y = 2$,$x = 5$;当$y = 4$,$x = 4$;当$y = 6$(不满足$2x>y$,舍去),
所以等腰三角形三边可以为$5,5,2$或$4,4,4$($4,4,4$也是等边三角形);
能搭成等边三角形,三边都为$4$根火柴。
示意图:
等腰三角形($5,5,2$):用$5$根火柴、$5$根火柴、$2$根火柴首尾顺次相接;
等边三角形:三边均用$4$根火柴首尾顺次相接。
(1) 不能;
(2) 能搭成等腰三角形:
设等腰三角形腰长为$x$根火柴,底长为$y$根火柴,
则$2x + y = 12$,
根据三角形三边关系$2x>y$且$|x - x|<y$(显然成立),
由$2x + y = 12$和$2x>y$,可得$12 - y>y$,$y < 6$,
同时$y>0$,且$x=\frac{12 - y}{2}$为正整数,
当$y = 2$,$x = 5$;当$y = 4$,$x = 4$;当$y = 6$(不满足$2x>y$,舍去),
所以等腰三角形三边可以为$5,5,2$或$4,4,4$($4,4,4$也是等边三角形);
能搭成等边三角形,三边都为$4$根火柴。
示意图:
等腰三角形($5,5,2$):用$5$根火柴、$5$根火柴、$2$根火柴首尾顺次相接;
等边三角形:三边均用$4$根火柴首尾顺次相接。
查看更多完整答案,请扫码查看


