第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
例 2 如图,已知 $ \triangle ABC $。
(1)用尺规作图方法作 $ AC $ 的垂直平分线 $ MN $,交 $ AB $ 于点 $ E $,交 $ AC $ 于点 $ D $,连接 $ CE $;(保留作图痕迹,不写作法)
(2)若 $ AD = 7 $,$ \triangle BCE $ 周长为 25,求 $ \triangle ABC $ 的周长。

名师导引 应用尺规作图时,要认真分析题意,结合几何图形,将问题转化为基本作图。
(1)用尺规作图方法作 $ AC $ 的垂直平分线 $ MN $,交 $ AB $ 于点 $ E $,交 $ AC $ 于点 $ D $,连接 $ CE $;(保留作图痕迹,不写作法)
(2)若 $ AD = 7 $,$ \triangle BCE $ 周长为 25,求 $ \triangle ABC $ 的周长。

名师导引 应用尺规作图时,要认真分析题意,结合几何图形,将问题转化为基本作图。
答案:
(2) 39
(2) 39
变式训练 如图,已知 $ \triangle ABC $,$ P $ 为边 $ BC $ 上一点($ BP < AB $),请用尺规作图的方法在边 $ AB $ 上求作一点 $ Q $,使 $ PQ + BQ = AB $。(保留作图痕迹,不写作法)


答案:
(作图痕迹如下:连接AP;分别以A、P为圆心,大于$\frac{1}{2}AP$长为半径画弧,两弧分别交于两点,过这两点作直线交AB于点Q),点Q即为所求。
1. 在巴黎奥运会射击混合团体 10 米气步枪比赛中,中国选手夺得本届奥运会的首枚金牌。如图是巴黎奥运会射击项目图标,这个图案的对称轴的条数为(

A.6
B.4
C.2
D.1
B
)
A.6
B.4
C.2
D.1
答案:
D(错误,正确答案为)B
2. 如图,在 $ \triangle ABC $ 中,分别以点 $ A $,$ C $ 为圆心,大于 $ \frac{1}{2}AC $ 长为半径画弧,两弧相交于点 $ D $,$ E $,作直线 $ DE $ 与 $ BC $ 交于点 $ F $,连接 $ AF $。若 $ AB = 6 $,$ BC = 7 $,则 $ \triangle ABF $ 的周长为(
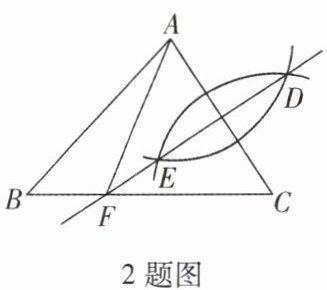
A.13
B.14
C.15
D.16
A
)
A.13
B.14
C.15
D.16
答案:
A
3. 如图,$ P $ 是 $ \angle ACB $ 外一点,$ D $,$ E $ 分别是 $ \angle ACB $ 两边上的点,点 $ P $ 关于 $ CA $ 的对称点 $ P_1 $ 恰好落在线段 $ ED $ 上,点 $ P $ 关于 $ CB $ 的对称点 $ P_2 $ 落在 $ ED $ 的延长线上。若 $ PE = 24 $,$ PD = 32 $,$ ED = 37 $,则线段 $ P_1P_2 $ 的长为
45
。
答案:
45
4. (1)如图,在 $ \triangle ABC $ 中,用尺规作 $ \angle ABC $ 的平分线 $ BD $ 与 $ AC $ 的垂直平分线 $ l $ 交于点 $ D $;(只保留作图痕迹)
(2)在(1)所作的图形中,连接 $ DA $,$ DC $,若 $ DC = AB $,探究 $ DA $ 与 $ BC $ 的位置关系,并说明理由。
请补全下面的解题过程:
解:$ DA // BC $。理由如下:
$ \because BD $ 平分 $ \angle ABC $,
$ \therefore $
$ \because l $ 是 $ AC $ 的垂直平分线,
$ \therefore $
$ \because DC = AB $,
$ \therefore $
$ \therefore \angle ADB = \angle ABD $。
$ \therefore $
$ \therefore AD // BC $。
(2)在(1)所作的图形中,连接 $ DA $,$ DC $,若 $ DC = AB $,探究 $ DA $ 与 $ BC $ 的位置关系,并说明理由。
请补全下面的解题过程:
解:$ DA // BC $。理由如下:

$ \because BD $ 平分 $ \angle ABC $,
$ \therefore $
$\angle ABD = \angle CBD$
。$ \because l $ 是 $ AC $ 的垂直平分线,
$ \therefore $
$DA = DC$
。$ \because DC = AB $,
$ \therefore $
$DA = AB$
。$ \therefore \angle ADB = \angle ABD $。
$ \therefore $
$\angle ADB = \angle CBD$
。$ \therefore AD // BC $。
答案:
(1)略(根据描述作图:先用尺规作$\angle ABC$的角平分线$BD$,再作$AC$的垂直平分线$l$,两者交点为$D$)
(2)解:$DA// BC$,理由如下:
$\because BD$平分$\angle ABC$,
$\therefore \angle ABD = \angle CBD$。
$\because l$是$AC$的垂直平分线,
$\therefore DA = DC$。
$\because DC = AB$,
$\therefore DA = AB$。
$\therefore\angle ADB = \angle ABD$。
$\therefore\angle ADB = \angle CBD$。
$\therefore AD// BC$。
故答案为$\angle ABD = \angle CBD$;$DA = DC$;$DA = AB$;$\angle ADB = \angle CBD$。
(2)解:$DA// BC$,理由如下:
$\because BD$平分$\angle ABC$,
$\therefore \angle ABD = \angle CBD$。
$\because l$是$AC$的垂直平分线,
$\therefore DA = DC$。
$\because DC = AB$,
$\therefore DA = AB$。
$\therefore\angle ADB = \angle ABD$。
$\therefore\angle ADB = \angle CBD$。
$\therefore AD// BC$。
故答案为$\angle ABD = \angle CBD$;$DA = DC$;$DA = AB$;$\angle ADB = \angle CBD$。
查看更多完整答案,请扫码查看


