《2025年学习指要八年级数学上册人教版》

变式训练 如图,工人师傅要检查人字梁的 $ \angle B $ 和 $ \angle C $ 是否相等,但他手边只有一个刻度尺. 他是这样操作的：①分别在 $ BA $ 和 $ CA $ 上取 $ BE = CG $；②在 $ BC $ 上取 $ BD = CF $；③连接 $ DE $,$ FG $,量出 $ DE $ 的长等于 $ FG $ 的长,则能说明 $ \angle B $ 和 $ \angle C $ 是相等的. 他的这种做法合理吗？为什么？

答案： 合理。
在△BDE和△CFG中，
∵BE=CG（已知），
BD=CF（已知），
DE=FG（已知），
∴△BDE≌△CFG（SSS），
∴∠B=∠C（全等三角形对应角相等）。

例3 如图,$ D $ 是 $ \triangle ABC $ 边 $ BC $ 上的一点,请用尺规在边 $ AC $ 上求作一点 $ E $,连接 $ BE $,使得 $ S _ { \triangle ABD } = S _ { \triangle ABE } $. (保留作图痕迹,不写作法)

名师导引 通过作 $ \angle EDC $ 等于 $ \angle ABC $,得 $ AB $ 的平行线,找平行线与 $ AC $ 的交点,依据同底等高的两三角形面积相等即可求点 $ E $.

答案： 作图步骤：
1. 以点 $ B $ 为圆心，任意长为半径画弧，分别交 $ BA $、$ BC $ 于点 $ M $、$ N $；
2. 以点 $ D $ 为圆心，$ BM $ 长为半径画弧，交 $ DC $ 于点 $ P $；
3. 以点 $ P $ 为圆心，$ MN $ 长为半径画弧，交前弧于点 $ Q $；
4. 作射线 $ DQ $，交 $ AC $ 于点 $ E $。
结论： 点 $ E $ 即为所求。
（注：保留作图痕迹，包括弧与交点标记。）

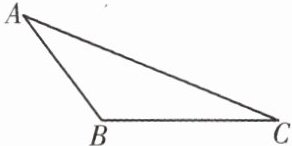
变式训练 如图,已知 $ \triangle ABC $,用尺规作 $ \triangle DEF $,使得 $ \triangle DEF \cong \triangle ABC $.
小明准备按以下作图步骤完成：
①作射线 $ EF $,在射线 $ EF $ 上截取 $ EF = $$BC$；
②以点 $ E $ 为圆心,以$AB$长为半径作弧,再以点 $ F $ 为圆心,以$AC$长为半径作弧,两弧交于点 $ D $；
③连接 $ DE $,$ DF $,$ \triangle DEF $ 即为所求(依据：$SSS$（边 - 边 - 边）).
请补全作图步骤及作图依据,并作出所求作三角形.

答案： ① $BC$；
② $AB$，$AC$；
③ $SSS$（边 - 边 - 边）。
作图步骤：先作射线$EF$，在射线$EF$上截取$EF = BC$；以点$E$为圆心，$AB$长为半径作弧，以点$F$为圆心，$AC$长为半径作弧，两弧交于点$D$；连接$DE$，$DF$，$\triangle DEF$即为所求。

1. (2024·河北唐山·期末)如图,在纸板上先任意画一个 $ \triangle ABC $,再画一个 $ \triangle DEF $,使 $ AB = DE $,$ AC = DF $,$ BC = EF $,将 $ \triangle DEF $ 剪下来,放到 $ \triangle ABC $ 上,它们完全重合吗？(A)

A.重合
B.不重合
C.不一定重合
D.无法判断

答案： A

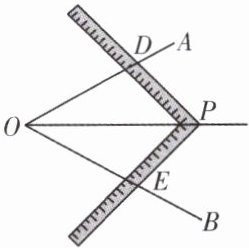
2. 工人师傅经常利用角尺平分一个任意角. 如图,$ \angle AOB $ 是一个任意角,在边 $ OA $,$ OB $ 上分别取 $ OD = OE $,移动角尺,使角尺两边相同的刻度分别与 $ D $,$ E $ 重合,这时过角尺顶点 $ P $ 的射线 $ OP $ 就是 $ \angle AOB $ 的平分线. 你认为工人师傅在此过程中用到的三角形全等的判定方法是(D)

A.SAS
B.ASA
C.AAS
D.SSS

答案： D