《2025年学习指要八年级数学上册人教版》

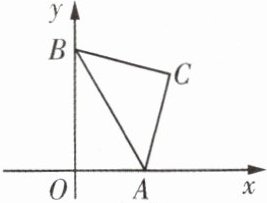
3. 如图,将一个含45度角的直角三角板的直角顶点放在直角坐标系中点C处,三角板另两个顶点分别落在x轴,y轴上的点A,B处,已知点C(3,3),则OA + OB的值为6.

答案： 6

4. 如图,某游乐园有两个长度相等的滑梯BC与EF,滑梯BC的高AC与滑梯EF水平方向的长度DF相等,∠DEF = 30°. 相关部门针对滑梯类儿童游乐设备作了严格的安全要求：在滑行方向上,要求整体滑行区与水平面的夹角应不大于40°. 滑梯BC与滑梯EF是否符合安全要求? 请说明理由.

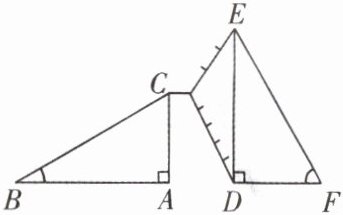
答案： 在Rt△ABC和Rt△EDF中（∠A=∠D=90°）：
已知BC=EF，AC=DF，
∴Rt△ABC≌Rt△EDF（HL），
∴∠ABC=∠DEF=30°。
滑梯BC：
在Rt△ABC中，∠ABC=30°＜40°，符合安全要求。
滑梯EF：
在Rt△EDF中，∠EFD=90°-∠DEF=60°＞40°，不符合安全要求。
结论：滑梯BC符合安全要求，滑梯EF不符合安全要求。

5. 在学习完三角形全等的判定方法(SAS,ASA,AAS,SSS)和直角三角形全等的判定方法(HL)后,小颖对“两边分别相等且其中一组等边的对角相等的两个三角形”的情形进行探究.
(1)【问题提出】P是∠MAN平分线上的点,在AM,AN上各取一点B,C. 如图1,若取PB = PC,AC ＞ AB,此时显然△APB与△APC不全等. 但是∠ABP与∠ACP有一定的数量关系,猜想∠ABP与∠ACP的关系为∠ABP+∠ACP=180°；
(2)【探究】小颖对图1继续进行研究,在图1的基础上添加辅助线得到了图2、图3,请你先在图2、图3中选择一个图形,并描述辅助线(即添加条件),再证明(1)的结论.
你选择图2,描述辅助线过点P作PF⊥AM于点F，PE⊥AN于点E.
写出证明过程：
证明：∵P是∠MAN平分线上的点，PF⊥AM，PE⊥AN
∴PF=PE（角的平分线上的点到角的两边的距离相等）
在Rt△PFB和Rt△PEC中，
$\left\{\begin{array}{l} PB=PC\\ PF=PE\end{array}\right.$
∴Rt△PFB≌Rt△PEC（HL）
∴∠PBF=∠PCE
∵PF⊥AM
∴∠PFB=90°
∴∠ABP+∠PBF=180°（平角的定义）
∵∠PCE=∠ACP
∴∠ABP+∠ACP=180°

答案：
(1)∠ABP+∠ACP=180°
(2)2；过点P作PF⊥AM于点F，PE⊥AN于点E
证明：
∵P是∠MAN平分线上的点，PF⊥AM，PE⊥AN
∴PF=PE（角的平分线上的点到角的两边的距离相等）
在Rt△PFB和Rt△PEC中，
$\left\{\begin{array}{l} PB=PC\\ PF=PE\end{array}\right.$
∴Rt△PFB≌Rt△PEC（HL）
∴∠PBF=∠PCE
∵PF⊥AM
∴∠PFB=90°
∴∠ABP+∠PBF=180°（平角的定义）
∵∠PCE=∠ACP
∴∠ABP+∠ACP=180°

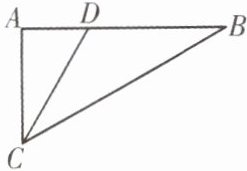
角的平分线的性质：角的平分线上的点到角的两边的距离相等.
思考 ①这里的距离是指该点到角的两边的垂线段的长.②该性质的条件是：一个点在角的平分线上,结论是：这个点到角两边的距离相等.
练习 如图,CD 是△ABC 的角平分线.若∠A = 90°,AD = $\sqrt{5}$,则点 D 到 BC 的距离是$\sqrt{5}$.

答案： 思考答案依次为：相等；垂线段；一个点在角的平分线上；这个点到角两边的距离相等；
练习：$\sqrt{5}$。