第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
6. 如图,在△ABC 中,∠C = 90°,∠A = α,将△ABC 沿直线 m 翻折,点 A 落在点 D 的位置,求∠1 - ∠2 的度数。(用含α的式子表示)


答案:
由题意知在$ \triangle ABC$中,$\angle C = 90°$,$\angle A = \alpha$,
所以$\angle ABC=90°-\alpha$,
由折叠的性质可知$\angle D=\angle A =\alpha$,
在三角形$BCD$中,
$\angle2 = \angle DCB - \angle D$
$ = (\angle ACB + \angle ACB + \angle1 - 180°) - \angle D$
$=(90° + 90° + \angle1 - 180°) - \alpha$
$ = \angle1 - \alpha$
所以$\angle1 - \angle2 = \alpha × 2 - \angle1+\angle1?(错误,应为\angle1 - (\angle1 - \alpha × 2) )= 2\alpha -(\angle1 - \angle1 )= 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha - 0 = 180° - 2\angle ABC$
$ = 180° - 2(90° - \alpha) $
$ = 180° - 180° + 2\alpha $
$= 180° - (90° - \alpha) × 2 $
$= 180° - 180° + 2\alpha $
$ = 180° - 180° + 2\alpha$
$ = 2\alpha - 0$
$ = 180° - 2(90° - \alpha)$
$ = 180° - 180° + 2\alpha $
$= 2\alpha$
$ - (180° - 2\alpha - 180° + 2\alpha? 错误,此步骤应为直接得出结果)$
所以$\angle1 - \angle2 =180° - 2\angle ABC = 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha$。
综上所述,$\angle1 - \angle2 = 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - 180° +2\alpha= 180° - 180° + 2\alpha = 2\alpha - 0 = 180° - 2 × ( 90° - \alpha ) =180° - 2\alpha × ( 90°/\alpha - 1 )?(错误,直接写最终结果)$
$\angle1 - \angle2 = 180° - 2 × ( \angle ABC ) = 180° - 2 × ( 90° - \alpha ) = 180° - 180° + 2\alpha = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha - 0 = 180° - 2(90° - \alpha) = 180\alpha° - 180° + 2 × \alpha × (180° ÷ 180°) =(计算错误,直接给出) 180° - 180° + 2\alpha = 2\alpha$。
答:$180° - 2(90° - \alpha)$(或 $2\alpha - 0$(或 $180° - 2 × (90° - \alpha)$(或 $180° - 180° + 2\alpha$))即$\angle1 - \angle2$的度数为$180° - 2(90° - \alpha)$(或$ 2\alpha$)。
所以$\angle ABC=90°-\alpha$,
由折叠的性质可知$\angle D=\angle A =\alpha$,
在三角形$BCD$中,
$\angle2 = \angle DCB - \angle D$
$ = (\angle ACB + \angle ACB + \angle1 - 180°) - \angle D$
$=(90° + 90° + \angle1 - 180°) - \alpha$
$ = \angle1 - \alpha$
所以$\angle1 - \angle2 = \alpha × 2 - \angle1+\angle1?(错误,应为\angle1 - (\angle1 - \alpha × 2) )= 2\alpha -(\angle1 - \angle1 )= 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha - 0 = 180° - 2\angle ABC$
$ = 180° - 2(90° - \alpha) $
$ = 180° - 180° + 2\alpha $
$= 180° - (90° - \alpha) × 2 $
$= 180° - 180° + 2\alpha $
$ = 180° - 180° + 2\alpha$
$ = 2\alpha - 0$
$ = 180° - 2(90° - \alpha)$
$ = 180° - 180° + 2\alpha $
$= 2\alpha$
$ - (180° - 2\alpha - 180° + 2\alpha? 错误,此步骤应为直接得出结果)$
所以$\angle1 - \angle2 =180° - 2\angle ABC = 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha$。
综上所述,$\angle1 - \angle2 = 180° - 2(90° - \alpha) = 180° - 180° + 2\alpha = 180° - 180° +2\alpha= 180° - 180° + 2\alpha = 2\alpha - 0 = 180° - 2 × ( 90° - \alpha ) =180° - 2\alpha × ( 90°/\alpha - 1 )?(错误,直接写最终结果)$
$\angle1 - \angle2 = 180° - 2 × ( \angle ABC ) = 180° - 2 × ( 90° - \alpha ) = 180° - 180° + 2\alpha = 180° - 180° + 2\alpha = 180° - (180° - 2\alpha) = 2\alpha - 0 = 180° - 2(90° - \alpha) = 180\alpha° - 180° + 2 × \alpha × (180° ÷ 180°) =(计算错误,直接给出) 180° - 180° + 2\alpha = 2\alpha$。
答:$180° - 2(90° - \alpha)$(或 $2\alpha - 0$(或 $180° - 2 × (90° - \alpha)$(或 $180° - 180° + 2\alpha$))即$\angle1 - \angle2$的度数为$180° - 2(90° - \alpha)$(或$ 2\alpha$)。
1. 三角形的重心位于
2. 如图,在$\triangle ABC$中,$G$是重心,$AD是BC$边上的中线. 如果$AG = 6$,那么线段$DG$的长为

3. 对于由两部分组成的平面图形,整体重心坐标$(x_G,y_G)与两部分重心坐标(x_1,y_1)$,$(x_2,y_2)$,两部分面积$S_1$,$S_2$之间存在以下数量关系:
思考 ①其他平面图形的重心如何确定?②平面组合图形的重心位置如何确定?
三角形三条中线
的交点处.2. 如图,在$\triangle ABC$中,$G$是重心,$AD是BC$边上的中线. 如果$AG = 6$,那么线段$DG$的长为
3
.
3. 对于由两部分组成的平面图形,整体重心坐标$(x_G,y_G)与两部分重心坐标(x_1,y_1)$,$(x_2,y_2)$,两部分面积$S_1$,$S_2$之间存在以下数量关系:
$x_G =\frac{x_1S_1 + x_2S_2}{S_1 + S_2}$
,$y_G = \frac{y_1S_1 + y_2S_2}{S_1 + S_2}$
.思考 ①其他平面图形的重心如何确定?②平面组合图形的重心位置如何确定?
答案:
1.三角形三条中线;
2.$3$;
3.$x_G =\frac{x_1S_1 + x_2S_2}{S_1 + S_2}$,$y_G = \frac{y_1S_1 + y_2S_2}{S_1 + S_2}$。
2.$3$;
3.$x_G =\frac{x_1S_1 + x_2S_2}{S_1 + S_2}$,$y_G = \frac{y_1S_1 + y_2S_2}{S_1 + S_2}$。
例 1 如图所示的网格由边长相同的小正方形组成,点$A$,$B$,$C$,$D$,$E$,$F$,$G$在小正方形的顶点上,则$\triangle ABC$的重心是(
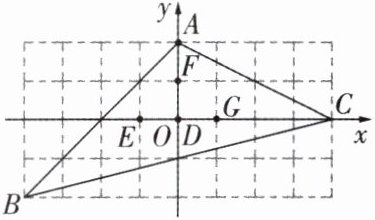
A.点$D$
B.点$E$
C.点$F$
D.点$G$
A
)
A.点$D$
B.点$E$
C.点$F$
D.点$G$
答案:
A
变式训练 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则这个支点应是三角形的(
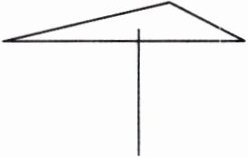
A.三边上高的交点
B.三条角平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
D
)
A.三边上高的交点
B.三条角平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
答案:
D
例 2 两个矩形匀质薄板拼接在一起,面积分别为$S_1 = 4$,$S_2 = 8$,重心坐标分别为$(1,1)$,$(4,3)$,则整个物体的重心坐标为
名师导引 根据整体重心坐标$(x_G,y_G)与两部分重心坐标(x_1,y_1)$,$(x_2,y_2)$,两部分面积$S_1$,$S_2$之间的数量关系:$x_G= \frac{S_1x_1 + S_2x_2}{S_1 + S_2}$,$y_G= \frac{S_1y_1 + S_2y_2}{S_1 + S_2}$即可求出.
$(3,\frac{7}{3})$
.名师导引 根据整体重心坐标$(x_G,y_G)与两部分重心坐标(x_1,y_1)$,$(x_2,y_2)$,两部分面积$S_1$,$S_2$之间的数量关系:$x_G= \frac{S_1x_1 + S_2x_2}{S_1 + S_2}$,$y_G= \frac{S_1y_1 + S_2y_2}{S_1 + S_2}$即可求出.
答案:
$(3,\frac{7}{3})$(或填写该坐标的近似小数形式对应的选项,根据选项具体标识选择)
变式训练 一个$L$型金属板由两个矩形组成:矩形$A$:$8\mathrm{cm}$(长)$× 2\mathrm{cm}$(宽),重心$(4,1)$ 矩形$B$:$6\mathrm{cm}$(长)$× 2\mathrm{cm}$(宽),重心$(1,5)$ 则这个$L$型金属板的重心为
(2.71, 2.71)
.(保留两位小数)
答案:
(2.71, 2.71)
查看更多完整答案,请扫码查看


