第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
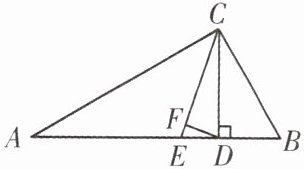
巩固提升 如图,在△ABC 中,∠A = 30°,∠B = 60°,CE 平分∠ACB.
(1)求∠ACE 的度数;
(2)CD⊥AB 于点 D,点 F 在 CE 上,∠CDF = 75°,求∠CFD 的度数.
(1)求∠ACE 的度数;
(2)CD⊥AB 于点 D,点 F 在 CE 上,∠CDF = 75°,求∠CFD 的度数.

答案:
(1)
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,已知$\angle A = 30^{\circ}$,$\angle B = 60^{\circ}$,则$\angle ACB=180^{\circ}-\angle A - \angle B=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$。
因为$CE$平分$\angle ACB$,所以$\angle ACE=\frac{1}{2}\angle ACB = 45^{\circ}$。
(2)
因为$CD\perp AB$,$\angle B = 60^{\circ}$,在$Rt\triangle BCD$中,$\angle BCD = 90^{\circ}-\angle B=90^{\circ}-60^{\circ}=30^{\circ}$。
由
(1)知$\angle ACE = 45^{\circ}$,所以$\angle DCF=\angle ACE-\angle BCD = 45^{\circ}-30^{\circ}=15^{\circ}$。
在$\triangle CDF$中,已知$\angle CDF = 75^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle CFD=180^{\circ}-\angle CDF-\angle DCF=180^{\circ}-75^{\circ}-15^{\circ}=90^{\circ}$。
综上,
(1)中$\angle ACE$的度数为$45^{\circ}$;
(2)中$\angle CFD$的度数为$90^{\circ}$。
(1)
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,已知$\angle A = 30^{\circ}$,$\angle B = 60^{\circ}$,则$\angle ACB=180^{\circ}-\angle A - \angle B=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$。
因为$CE$平分$\angle ACB$,所以$\angle ACE=\frac{1}{2}\angle ACB = 45^{\circ}$。
(2)
因为$CD\perp AB$,$\angle B = 60^{\circ}$,在$Rt\triangle BCD$中,$\angle BCD = 90^{\circ}-\angle B=90^{\circ}-60^{\circ}=30^{\circ}$。
由
(1)知$\angle ACE = 45^{\circ}$,所以$\angle DCF=\angle ACE-\angle BCD = 45^{\circ}-30^{\circ}=15^{\circ}$。
在$\triangle CDF$中,已知$\angle CDF = 75^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle CFD=180^{\circ}-\angle CDF-\angle DCF=180^{\circ}-75^{\circ}-15^{\circ}=90^{\circ}$。
综上,
(1)中$\angle ACE$的度数为$45^{\circ}$;
(2)中$\angle CFD$的度数为$90^{\circ}$。
例 3 如图,已知∠B = ∠ADB,∠C = ∠CAD,若∠BAC = 78°,求∠BAD 的度数.
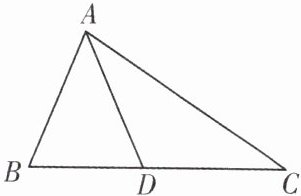
名师导引 可以设∠C = ∠CAD = x,利用三角形外角的性质表示出其余的角,再借助三角形内角和为 180°建立方程. 在角的求值问题中,常常利用图形关系或内角、外角之间的关系进行转化,然后利用三角形内角和定理列方程求解.

名师导引 可以设∠C = ∠CAD = x,利用三角形外角的性质表示出其余的角,再借助三角形内角和为 180°建立方程. 在角的求值问题中,常常利用图形关系或内角、外角之间的关系进行转化,然后利用三角形内角和定理列方程求解.
答案:
设$\angle C = \angle CAD = x$。
根据三角形外角性质,$\angle ADB=\angle C+\angle CAD = 2x$。
因为$\angle B = \angle ADB$,所以$\angle B = 2x$。
在$\triangle ABC$中,$\angle B + \angle BAC+\angle C = 180^{\circ}$,已知$\angle BAC = 78^{\circ}$,则$2x + 78^{\circ}+x = 180^{\circ}$。
$3x=180^{\circ}-78^{\circ}=102^{\circ}$,解得$x = 34^{\circ}$。
$\angle BAD=\angle BAC-\angle CAD=78^{\circ}- 34^{\circ}=44^{\circ}$。
综上,$\angle BAD$的度数为$44^{\circ}$。
根据三角形外角性质,$\angle ADB=\angle C+\angle CAD = 2x$。
因为$\angle B = \angle ADB$,所以$\angle B = 2x$。
在$\triangle ABC$中,$\angle B + \angle BAC+\angle C = 180^{\circ}$,已知$\angle BAC = 78^{\circ}$,则$2x + 78^{\circ}+x = 180^{\circ}$。
$3x=180^{\circ}-78^{\circ}=102^{\circ}$,解得$x = 34^{\circ}$。
$\angle BAD=\angle BAC-\angle CAD=78^{\circ}- 34^{\circ}=44^{\circ}$。
综上,$\angle BAD$的度数为$44^{\circ}$。
巩固提升 如图,在△ABC 中,AB = AC,D,E 分别在边 AC,AB 上,且 BC = BD,AD = DE = EB,求∠A 的度数.
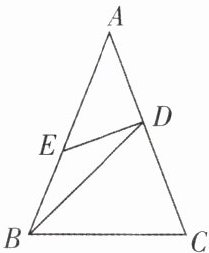

答案:
设∠A=x。
∵AD=DE,
∴∠AED=∠A=x(等边对等角),
∴∠ADE=180°-∠A-∠AED=180°-2x(三角形内角和定理)。
∵DE=EB,设∠EBD=∠EDB=y,
∴∠DEB=180°-2y(三角形内角和定理)。
∵A,E,B共线,
∴∠AED+∠DEB=180°,即x+180°-2y=180°,得x=2y,
∴y= x/2。
∵AB=AC,
∴∠ABC=∠ACB(等边对等角),设∠ABC=∠ACB=z,
则∠DBC=∠ABC-∠EBD=z - x/2。
∵BC=BD,
∴∠BDC=∠ACB=z(等边对等角)。
在△BDC中,∠DBC+∠BCD+∠BDC=180°,即(z - x/2)+z+z=180°,得3z - x/2=180°①。
在△ABC中,∠A+∠ABC+∠ACB=180°,即x+2z=180°,得z=(180°-x)/2②。
将②代入①:3×(180°-x)/2 - x/2=180°,
化简得270°-2x=180°,解得x=45°。
∠A=45°。
∵AD=DE,
∴∠AED=∠A=x(等边对等角),
∴∠ADE=180°-∠A-∠AED=180°-2x(三角形内角和定理)。
∵DE=EB,设∠EBD=∠EDB=y,
∴∠DEB=180°-2y(三角形内角和定理)。
∵A,E,B共线,
∴∠AED+∠DEB=180°,即x+180°-2y=180°,得x=2y,
∴y= x/2。
∵AB=AC,
∴∠ABC=∠ACB(等边对等角),设∠ABC=∠ACB=z,
则∠DBC=∠ABC-∠EBD=z - x/2。
∵BC=BD,
∴∠BDC=∠ACB=z(等边对等角)。
在△BDC中,∠DBC+∠BCD+∠BDC=180°,即(z - x/2)+z+z=180°,得3z - x/2=180°①。
在△ABC中,∠A+∠ABC+∠ACB=180°,即x+2z=180°,得z=(180°-x)/2②。
将②代入①:3×(180°-x)/2 - x/2=180°,
化简得270°-2x=180°,解得x=45°。
∠A=45°。
1. 以下列各组线段为边,能组成三角形的是(
A.2 cm,3 cm,5 cm
B.5 cm,6 cm,10 cm
C.1 cm,1 cm,3 cm
D.3 cm,4 cm,9 cm
B
)A.2 cm,3 cm,5 cm
B.5 cm,6 cm,10 cm
C.1 cm,1 cm,3 cm
D.3 cm,4 cm,9 cm
答案:
B
2. (跨学科融合)光线在镜面上反射时,经过入射点与镜面垂直的直线是法线,反射光线与法线的夹角等于入射光线与法线的夹角. 如图,两束光线$ l_1,l_2 $分别从不同方向射向镜面 m,入射点为$ A,B,n_1,n_2 $是法线$. l_1,l_2 $的反射光线相交于点 C. 若∠1 = 30°,∠2 = 50°,则∠ACB 的度数是(
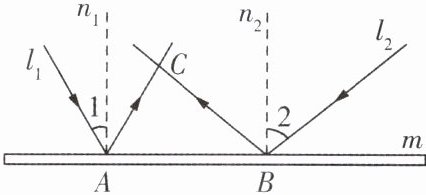
A.30°
B.50°
C.80°
D.90°
C
)
A.30°
B.50°
C.80°
D.90°
答案:
C
3. 如图,将三角形纸片 ABC 沿 DE 折叠,点 A 落在点 F 处,已知∠1 + ∠2 = 100°,则∠A 的度数为(
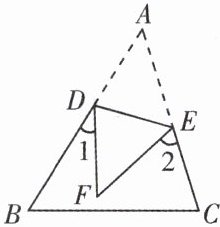
A.80°
B.100°
C.50°
D.以上都不对
C
)
A.80°
B.100°
C.50°
D.以上都不对
答案:
C
4. 下列条件:①∠A + ∠B = ∠C;②∠A:∠B:∠C = 5:3:2;③∠A = 90° - ∠B;④∠A = 2∠B = 3∠C;⑤∠A = $\frac{1}{3}$∠B = $\frac{1}{3}$∠C. 其中能确定△ABC 是直角三角形的有(
A.2 个
B.3 个
C.4 个
D.5 个
B
)A.2 个
B.3 个
C.4 个
D.5 个
答案:
B
5. 等腰三角形的周长为 17 cm,一边长为 4 cm,则其底边长为
4
cm.
答案:
4
查看更多完整答案,请扫码查看


