第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
直角三角形中,如果一个角等于 $30^{\circ}$,那么它所对的直角边等于
思考 ①有哪些方法可以证明上述结论?
②直角三角形中,如果一条直角边是斜边的一半,那么这条直角边所对的角是 $30^{\circ}$ 吗?
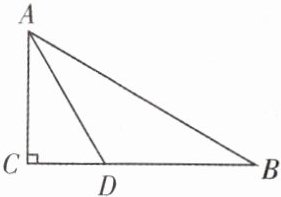
填空 如图,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AD$ 平分 $\angle BAC$ 交 $BC$ 于 $D$,$CD = 3$,则 $DB = $
斜边
的一半。思考 ①有哪些方法可以证明上述结论?
②直角三角形中,如果一条直角边是斜边的一半,那么这条直角边所对的角是 $30^{\circ}$ 吗?
填空 如图,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AD$ 平分 $\angle BAC$ 交 $BC$ 于 $D$,$CD = 3$,则 $DB = $
6
。
答案:
斜边;①见解析;②是;6
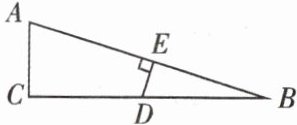
例 1 如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle B = 15^{\circ}$,$AB$ 的垂直平分线交 $BC$ 于 $D$,交 $AB$ 于 $E$,若 $DB = 10\ cm$,则 $AC = $
名师导引 将垂直平分线上的点与线段的两端点连接,可构造等腰三角形。
5 cm
。
名师导引 将垂直平分线上的点与线段的两端点连接,可构造等腰三角形。
答案:
连接$AD$,
因为$DE$是$AB$的垂直平分线,
所以$AD = BD = 10 cm$,
则$\angle B = \angle BAD = 15^{\circ}$,
所以$\angle ADC = \angle B + \angle BAD = 30^{\circ}$。
在$Rt\triangle ACD$中,
$\angle C = 90^{\circ}$,$\angle ADC = 30^{\circ}$,
所以$AC =\frac{1}{2} AD = 5 cm$。
故本题答案为$5 cm$。
因为$DE$是$AB$的垂直平分线,
所以$AD = BD = 10 cm$,
则$\angle B = \angle BAD = 15^{\circ}$,
所以$\angle ADC = \angle B + \angle BAD = 30^{\circ}$。
在$Rt\triangle ACD$中,
$\angle C = 90^{\circ}$,$\angle ADC = 30^{\circ}$,
所以$AC =\frac{1}{2} AD = 5 cm$。
故本题答案为$5 cm$。
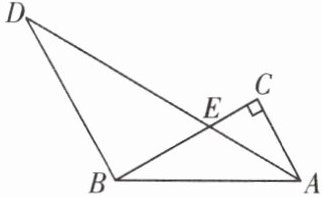
变式训练 如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle ABC = 30^{\circ}$,线段 $AD$ 平分 $\angle BAC$ 交 $BC$ 于点 $E$,又 $BD// AC$。求证:
(1) $AE = BE$;
(2) $BC + CE = DE$。
(1) $AE = BE$;
(2) $BC + CE = DE$。

答案:
(1) 在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\angle ABC=30^{\circ}$,$\therefore \angle BAC=60^{\circ}$。
$\because AD$平分$\angle BAC$,$\therefore \angle BAE=\frac{1}{2}\angle BAC=30^{\circ}$。
$\because \angle ABE=\angle ABC=30^{\circ}$,$\therefore \angle BAE=\angle ABE$。
$\therefore AE=BE$。
(2) $\because BD// AC$,$\angle C=90^{\circ}$,$\therefore \angle DBC=\angle C=90^{\circ}$(两直线平行,内错角相等)。
由角平分线定理,$\frac{BE}{EC}=\frac{AB}{AC}=2$($Rt\triangle ABC$中,$\angle ABC=30^{\circ}$,$AB=2AC$),$\therefore BE=2EC$,设$EC=a$,则$BE=2a$,$BC=BE+EC=3a$。
在$Rt\triangle AEC$中,$\angle EAC=30^{\circ}$,$\angle C=90^{\circ}$,$\therefore \angle AEC=60^{\circ}$,$\therefore \angle DEB=\angle AEC=60^{\circ}$(对顶角相等)。
在$Rt\triangle DBE$中,$\angle DEB=60^{\circ}$,$\angle DBC=90^{\circ}$,$\therefore \angle EDB=30^{\circ}$,$\therefore DE=2BE=4a$(直角三角形中$30^{\circ}$角所对直角边是斜边一半)。
$\because BC+CE=3a+a=4a$,$\therefore BC+CE=DE$。
(1) 在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\angle ABC=30^{\circ}$,$\therefore \angle BAC=60^{\circ}$。
$\because AD$平分$\angle BAC$,$\therefore \angle BAE=\frac{1}{2}\angle BAC=30^{\circ}$。
$\because \angle ABE=\angle ABC=30^{\circ}$,$\therefore \angle BAE=\angle ABE$。
$\therefore AE=BE$。
(2) $\because BD// AC$,$\angle C=90^{\circ}$,$\therefore \angle DBC=\angle C=90^{\circ}$(两直线平行,内错角相等)。
由角平分线定理,$\frac{BE}{EC}=\frac{AB}{AC}=2$($Rt\triangle ABC$中,$\angle ABC=30^{\circ}$,$AB=2AC$),$\therefore BE=2EC$,设$EC=a$,则$BE=2a$,$BC=BE+EC=3a$。
在$Rt\triangle AEC$中,$\angle EAC=30^{\circ}$,$\angle C=90^{\circ}$,$\therefore \angle AEC=60^{\circ}$,$\therefore \angle DEB=\angle AEC=60^{\circ}$(对顶角相等)。
在$Rt\triangle DBE$中,$\angle DEB=60^{\circ}$,$\angle DBC=90^{\circ}$,$\therefore \angle EDB=30^{\circ}$,$\therefore DE=2BE=4a$(直角三角形中$30^{\circ}$角所对直角边是斜边一半)。
$\because BC+CE=3a+a=4a$,$\therefore BC+CE=DE$。
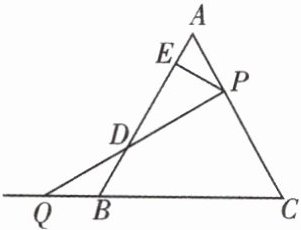
例 2 如图,在等边三角形 $ABC$ 中,$AB = 6$,$P$ 是 $AC$ 边上任意一点(与 $A$,$C$ 两点不重合),$Q$ 是 $CB$ 延长线上一点,$BQ = AP$,连接 $PQ$ 交 $AB$ 于 $D$,过 $P$ 作 $PE\perp AB$ 于 $E$。当 $\angle CQP = 30^{\circ}$ 时,求 $AP$ 的长。
名师导引 观察图形,结合已知条件,充分利用等边三角形及含 $30^{\circ}$ 角的直角三角形的性质,建立有关线段的数量关系,也可通过添加辅助线构造全等三角形解决问题。
变式训练 例 2 中,去掉“$\angle CQP = 30^{\circ}$”这一条件,求证:$DE = \frac{1}{2}AB$。

名师导引 观察图形,结合已知条件,充分利用等边三角形及含 $30^{\circ}$ 角的直角三角形的性质,建立有关线段的数量关系,也可通过添加辅助线构造全等三角形解决问题。
变式训练 例 2 中,去掉“$\angle CQP = 30^{\circ}$”这一条件,求证:$DE = \frac{1}{2}AB$。
答案:
解:过$P$作$PF// BC$交$AB$于$F$。
因为$\triangle ABC$是等边三角形,所以$\angle A=\angle ABC = \angle C = 60^{\circ}$。
因为$PF// BC$,所以$\angle AFP=\angle ABC = 60^{\circ}$,$\angle APF=\angle C = 60^{\circ}$。
所以$\triangle APF$是等边三角形,所以$AP = PF$。
又因为$BQ = AP$,所以$PF = BQ$。
因为$PF// BC$,所以$\angle PFD=\angle QBD$,$\angle FPD=\angle BQD$。
在$\triangle PFD$和$\triangle QBD$中:
$\begin{cases}\angle PFD=\angle QBD\\\angle FPD=\angle BQD\\PF = BQ\end{cases}$
所以$\triangle PFD\cong\triangle QBD(AAS)$,所以$FD = BD$。
因为$PE\perp AB$,$\triangle APF$是等边三角形,所以$AE = EF$(等边三角形三线合一)。
所以$DE=EF + FD=\frac{1}{2}AF+\frac{1}{2}FB=\frac{1}{2}(AF + FB)=\frac{1}{2}AB$。
综上,$DE = \frac{1}{2}AB$得证。
因为$\triangle ABC$是等边三角形,所以$\angle A=\angle ABC = \angle C = 60^{\circ}$。
因为$PF// BC$,所以$\angle AFP=\angle ABC = 60^{\circ}$,$\angle APF=\angle C = 60^{\circ}$。
所以$\triangle APF$是等边三角形,所以$AP = PF$。
又因为$BQ = AP$,所以$PF = BQ$。
因为$PF// BC$,所以$\angle PFD=\angle QBD$,$\angle FPD=\angle BQD$。
在$\triangle PFD$和$\triangle QBD$中:
$\begin{cases}\angle PFD=\angle QBD\\\angle FPD=\angle BQD\\PF = BQ\end{cases}$
所以$\triangle PFD\cong\triangle QBD(AAS)$,所以$FD = BD$。
因为$PE\perp AB$,$\triangle APF$是等边三角形,所以$AE = EF$(等边三角形三线合一)。
所以$DE=EF + FD=\frac{1}{2}AF+\frac{1}{2}FB=\frac{1}{2}(AF + FB)=\frac{1}{2}AB$。
综上,$DE = \frac{1}{2}AB$得证。
查看更多完整答案,请扫码查看


