《2025年学习指要八年级数学上册人教版》

1. 下列从左到右的变形,是因式分解的是(D)
A.$(3 - x)(3 + x) = 9 - x^2$
B.$(y + 1)(y - 3) = -(3 - y)(y + 1)$
C.$4yz - 2y^2z + z = 2y(2z - yz) + z$
D.$-8x^2 + 8x - 2 = -2(2x - 1)^2$

答案： D

2. 把多项式 $x^2 + ax + b$ 分解因式,得 $(x + 1)(x - 3)$,则 $a$,$b$ 的值分别是(B)
A.$2$,$3$
B.$-2$,$-3$
C.$-2$,$3$
D.$2$,$-3$

答案： B

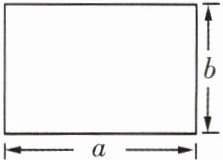
3. 如图,边长为 $a$,$b$ 的长方形的周长为 $14$,面积为 $12$,则 $a^3b + ab^3$ 的值为300。

答案： 300

4. 将下列各式分解因式：
(1) $3ab^2 - a^2b$；
(2) $a^2b - 2ab + b$；
(3) $3ma^3 + 6ma^2 - 12ma$；
(4) $(x + 2)^2 + 2(x + 2)$；
(5) $2m(m - n) + 4(n - m)$。

答案：
(1)
解：原式 $3ab^{2}-a^{2}b=ab(3b - a)$。
(2)
解：原式 $a^{2}b - 2ab + b=b(a^{2}-2a + 1)=b(a - 1)^{2}$。
(3)
解：原式 $3ma^{3}+6ma^{2}-12ma=3ma(a^{2}+2a - 4)$。
(4)
解：原式 $(x + 2)^{2}+2(x + 2)=(x + 2)(x + 2 + 2)=(x + 2)(x+4)$。
(5)
解：原式 $2m(m - n)+4(n - m)=2m(m - n)-4(m - n)=2(m - n)(m - 2)$。

5. $32×3.14 + 5.4×31.4 + 0.14×314 = $314。

答案： 314

6. 若 $x^2 + 2x - 2 = 0$,求代数式 $x^4 + 2x^3 - 3x^2 - 2x + 1$ 的值。

答案： 由已知 $x^{2} + 2x - 2 = 0$，可得 $x^{2} + 2x = 2$。
$x^{4} + 2x^{3} - 3x^{2} - 2x + 1$
$=(x^{4} + 2x^{3} - 2x^{2})- x^{2} - 2x + 1$
$=x^{2}(x^{2} + 2x - 2)- (x^{2} + 2x)+ 1$
把 $x^{2} + 2x = 2$ 代入上式可得：
原式 $=x^{2}×0 - 2 + 1$
$=-1$
综上，代数式 $x^{4} + 2x^{3} - 3x^{2} - 2x + 1$ 的值为 $-1$。

7. (1) 三角形的三边 $a$,$b$,$c$ 满足 $a(b - c) + 2(b - c) = 0$,则这个三角形的形状是等腰三角形。
(2) 三角形的三边 $a$,$b$,$c$ 满足 $a^2 - 2ab + b^2 = ac - bc$,则这个三角形的形状是等腰三角形。

答案：
(1)等腰三角形；
(2)等腰三角形。

平方差公式：$a^{2}-b^{2}=$$(a + b)(a - b)$。
思考 若一个代数式能用平方差公式分解因式,那么该代数式有什么特点？
填空 $25 - x^{2}= ($5$)^{2}-($x$)^{2}$；$9a^{4}-4b^{2}= ($$3a^{2}$$)^{2}-($$2b$$)^{2}$。

答案： 平方差公式：$a^{2} - b^{2} = (a + b)(a - b)$；
该代数式的特点是由两项组成，且这两项均为平方形式，同时符号相反；
$25 - x^{2} = (5)^{2} - (x)^{2}$；
$9a^{4} - 4b^{2} = (3a^{2})^{2} - (2b)^{2}$。

例 1 分解因式：
(1)$x^{2}-\frac{1}{9}$；
(2)$-4x^{2}+(2x - 3y)^{2}$；
(3)$25(a + b)^{2}-4a^{2}$。
名师导引 根据平方差公式的结构特征,找出对应于公式中的 $a,b$ 项是解决问题的关键,同时注意分解要彻底。

答案：
(1)
$\begin{aligned}x^{2}-\frac{1}{9} \\=x^{2}-(\frac{1}{3})^{2}\\=(x+\frac{1}{3})(x - \frac{1}{3})\end{aligned}$
(2)
$\begin{aligned}-4x^{2}+(2x - 3y)^{2}\\=(2x - 3y)^{2}-(2x)^{2}\\=(2x - 3y + 2x)(2x - 3y - 2x)\\=(4x - 3y)(-3y)\\=-3y(4x - 3y)\end{aligned}$
(3)
$\begin{aligned}25(a + b)^{2}-4a^{2}\\=[5(a + b)]^{2}-(2a)^{2}\\=(5a + 5b + 2a)(5a + 5b - 2a)\\=(7a + 5b)(3a + 5b)\end{aligned}$