《2025年学习指要八年级数学上册人教版》

5. 如图,社区计划在某小区建一个智能垃圾分类投放点 $ P $,需要满足以下条件：
(1)附近的两栋住宅楼 $ A $,$ B $ 到智能垃圾分类投放点 $ P $ 的距离相等,需要作出垂直平分线(填“角平分线”或“垂直平分线”)；
(2)点 $ P $ 到两条道路 $ OM $,$ ON $ 的距离相等,需要作出角平分线(填“角平分线”或“垂直平分线”)；
(3)请在图中利用尺规作图(保留作图痕迹,不写作法),确定点 $ P $ 的位置。
（尺规作图痕迹：作出线段AB的垂直平分线，作出∠MON的角平分线，两线交点即为点P）

答案：
(1)垂直平分线
(2)角平分线
(3)（尺规作图痕迹：作出线段AB的垂直平分线，作出∠MON的角平分线，两线交点即为点P）

6. (数学与生活)先阅读下文,再回答问题：
你也许很喜欢台球,玩台球的过程中也要用到数学知识。如图,四边形 $ ABCD $ 是一矩形台面,有两个球分别位于点 $ P $,$ Q $,先找出 $ P $ 点关于 $ CD $ 的对称点 $ P' $,连接 $ P'Q $ 交 $ CD $ 于 $ M $ 点,将 $ P $ 处的球击向点 $ M $ 经 $ CD $ 反弹后,会击中 $ Q $ 处的球。
请回答：如果使 $ P $ 处的球先碰撞台边 $ CD $ 反弹又碰撞台边 $ AB $ 后,再击中 $ Q $
处的球,应如何走位呢？(画出图形)

答案： 1. 作点P关于CD的对称点P'；
2. 作点Q关于AB的对称点Q'；
3. 连接P'Q'，交CD于点M，交AB于点N；
4. 击球路径为P→M→N→Q。
（图形：在矩形ABCD中，作出P关于CD对称点P'，Q关于AB对称点Q'，连接P'Q'分别交CD于M、AB于N，连接PM、MN、NQ）

由一个平面图形可以得到与它关于某条直线 $ l $ 对称的图形,此图形与原图形全等;对称图形上的每一点都是原图形上的某一点关于直线 $ l $ 的对称点.
思考 你有哪些方法可以画出一个图形关于某条直线对称的图形?

答案： 此图形与原图形全等；对称点

例 1 作出下列图形关于直线 $ l $ 的对称图形.

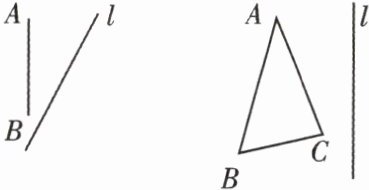
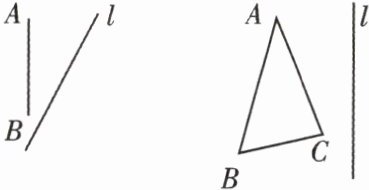
名师导引 作已知图形关于某直线的对称图形,先作已知图形各个关键点的对称点,再顺次连接各点就可得到对称图形.其中作点的对称点的方法:作垂线,顺延长,取相等.

答案： 本题可根据“作点的对称点的方法：作垂线，顺延长，取相等”，先作出原图形各个关键点关于直线$l$的对称点，再顺次连接各对称点，从而得到对称图形。
步骤一：作点$A$关于直线$l$的对称点$A'$
过点$A$作直线$l$的垂线，垂足为$O$，在垂线上延长$AO$到$A'$，使$A'O = AO$，则点$A'$即为点$A$关于直线$l$的对称点。
步骤二：作点$B$关于直线$l$的对称点$B'$
过点$B$作直线$l$的垂线，垂足为$P$，在垂线上延长$BP$到$B'$，使$B'P = BP$，则点$B'$即为点$B$关于直线$l$的对称点。
步骤三：作点$C$关于直线$l$的对称点$C'$
过点$C$作直线$l$的垂线，垂足为$Q$，在垂线上延长$CQ$到$C'$，使$C'Q = CQ$，则点$C'$即为点$C$关于直线$l$的对称点。
步骤四：连接对称点得到对称图形
顺次连接$A'$、$B'$、$C'$，得到$\triangle A'B'C'$，则$\triangle A'B'C'$就是$\triangle ABC$关于直线$l$的对称图形。
（实际作答时需在答题卡上准确画出对称图形）。

变式训练 作出 $ \triangle ABC $ 关于直线 $ AM $ 的对称图形.

答案： 作法如下：
1. 分别过点 $B$，点 $C$ 作直线 $AM$ 的垂线，垂足分别为点 $D$，点 $E$。
2. 分别延长 $BD$，$CE$ 至点 $B'$，点 $C'$，使 $B'D = BD$，$C'E = CE$。
3. 顺次连接 $A$，$C'$，$B'$，则$\triangle AB'C'$ 就是 $\triangle ABC$ 关于直线 $AM$ 的对称图形。