第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
证明两直角三角形全等,利用“HL”是最简单的方法,但切记要在表示三角形的符号“△”前面加上“Rt”.
答案:
假设题目为:如图,在$Rt\triangle ABC$和$Rt\triangle DEF$中,$\angle C = \angle F = 90^{\circ}$,$AC = DF$,$AB = DE$,求证:$Rt\triangle ABC ≌ Rt\triangle DEF$。
答题:
在$Rt\triangle ABC$和$Rt\triangle DEF$中,
由于$\angle C = \angle F = 90^{\circ}$,
$AC = DF$(已知),
$AB = DE$(已知),
根据$HL$全等判定,在直角三角形中,如果一条直角边和斜边分别相等,则这两个直角三角形全等。
因此,$Rt\triangle ABC ≌ Rt\triangle DEF(HL)$。
答题:
在$Rt\triangle ABC$和$Rt\triangle DEF$中,
由于$\angle C = \angle F = 90^{\circ}$,
$AC = DF$(已知),
$AB = DE$(已知),
根据$HL$全等判定,在直角三角形中,如果一条直角边和斜边分别相等,则这两个直角三角形全等。
因此,$Rt\triangle ABC ≌ Rt\triangle DEF(HL)$。
如图,已知∠A = ∠D = 90°,E,F在线段BC上,DE与AF交于点O,且AB = CD,BE = CF. 求证:Rt△ABF≌Rt△DCE.
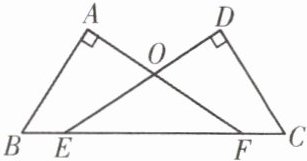

答案:
证明:
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE。
∵∠A=∠D=90°,
∴△ABF和△DCE都是直角三角形。
在Rt△ABF和Rt△DCE中,
∵AB=CD,BF=CE,
∴Rt△ABF≌Rt△DCE(HL)。
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE。
∵∠A=∠D=90°,
∴△ABF和△DCE都是直角三角形。
在Rt△ABF和Rt△DCE中,
∵AB=CD,BF=CE,
∴Rt△ABF≌Rt△DCE(HL)。
探究二 直角三角形全等的综合应用
例2 如图,已知∠ABC = ∠ADC = 90°,CB = CD,M是AC上任意一点. 求证:BM = DM.
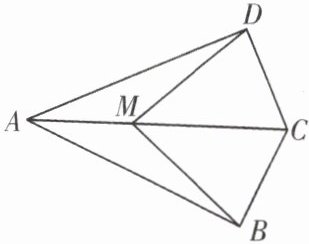
例2 如图,已知∠ABC = ∠ADC = 90°,CB = CD,M是AC上任意一点. 求证:BM = DM.

答案:
证明:
在Rt△ABC和Rt△ADC中,
∵CB=CD,AC=AC,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BCA=∠DCA。
在△BCM和△DCM中,
∵CB=CD,∠BCM=∠DCM,CM=CM,
∴△BCM≌△DCM(SAS),
∴BM=DM。
在Rt△ABC和Rt△ADC中,
∵CB=CD,AC=AC,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BCA=∠DCA。
在△BCM和△DCM中,
∵CB=CD,∠BCM=∠DCM,CM=CM,
∴△BCM≌△DCM(SAS),
∴BM=DM。
如图,过射线EF外一点D,作DE⊥EF,点A为射线EF上一点,在AF上截取AC = DE,作MC⊥EC,点D,M位于EF的同侧,连接AD,以A为圆心,AD长为半径画弧,交MC于B. 求证:
(1) △DAE≌△ABC;
(2) AD⊥AB.
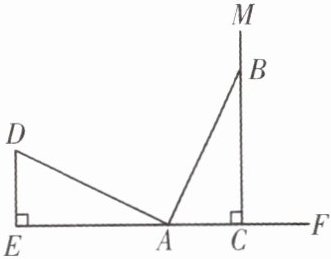
(1) △DAE≌△ABC;
(2) AD⊥AB.

答案:
(1)
∵DE⊥EF,
∴∠DEA=90°(垂直定义).
∵MC⊥EF,
∴∠ACB=90°(垂直定义).
∴△DAE和△ABC均为直角三角形.
由题意,AC=DE,AB=AD(以A为圆心AD为半径画弧,故AB=AD).
在Rt△DAE和Rt△ABC中,
$\left\{\begin{array}{l}AD=AB\\ DE=AC\end{array}\right.$
∴Rt△DAE≌Rt△ABC(HL).
(2)
∵△DAE≌△ABC,
∴∠DAE=∠ABC(全等三角形对应角相等).
在Rt△ABC中,∠ACB=90°,
∴∠ABC+∠BAC=90°(直角三角形两锐角互余).
∴∠DAE+∠BAC=90°(等量代换).
∵∠DAE+∠BAC=∠DAB,
∴∠DAB=90°,即AD⊥AB(垂直定义).
(1)
∵DE⊥EF,
∴∠DEA=90°(垂直定义).
∵MC⊥EF,
∴∠ACB=90°(垂直定义).
∴△DAE和△ABC均为直角三角形.
由题意,AC=DE,AB=AD(以A为圆心AD为半径画弧,故AB=AD).
在Rt△DAE和Rt△ABC中,
$\left\{\begin{array}{l}AD=AB\\ DE=AC\end{array}\right.$
∴Rt△DAE≌Rt△ABC(HL).
(2)
∵△DAE≌△ABC,
∴∠DAE=∠ABC(全等三角形对应角相等).
在Rt△ABC中,∠ACB=90°,
∴∠ABC+∠BAC=90°(直角三角形两锐角互余).
∴∠DAE+∠BAC=90°(等量代换).
∵∠DAE+∠BAC=∠DAB,
∴∠DAB=90°,即AD⊥AB(垂直定义).
1. 在课堂上,老师发给每人一张印有Rt△ABC(如图)的卡片,然后要求同学们画一个Rt△A'B'C',使得Rt△A'B'C'≌Rt△ABC,小赵和小刘同学先画出了∠MB'N = 90°之后,后续画图的主要过程分别如图所示. 以下对这两种画法的描述错误的是(
 A. 小赵同学作图判定Rt△A'B'C'≌Rt△ABC的依据是HL
A. 小赵同学作图判定Rt△A'B'C'≌Rt△ABC的依据是HL
B. 小赵同学第二步作图时,用圆规截取的长度是线段AC的长
C. 小刘同学作图判定Rt△A'B'C'≌Rt△ABC的依据是SAS
D. 小刘同学第一步作图时,用圆规截取的长度是线段AC的长
D
) A. 小赵同学作图判定Rt△A'B'C'≌Rt△ABC的依据是HL
A. 小赵同学作图判定Rt△A'B'C'≌Rt△ABC的依据是HLB. 小赵同学第二步作图时,用圆规截取的长度是线段AC的长
C. 小刘同学作图判定Rt△A'B'C'≌Rt△ABC的依据是SAS
D. 小刘同学第一步作图时,用圆规截取的长度是线段AC的长
答案:
D
2. 如图,∠B = ∠D = 90°,AB = AD,∠1 = 25°,则∠2的度数为(
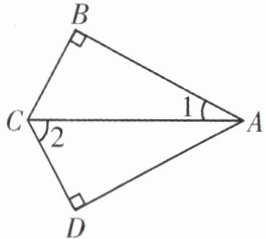
A.25°
B.40°
C.65°
D.60°
C
)
A.25°
B.40°
C.65°
D.60°
答案:
C
查看更多完整答案,请扫码查看


