第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
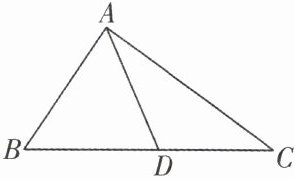
例 1 如图,点 D 在△ABC 的 BC 边上.
(1)作∠ADB 和∠ADC 的平分线 DM 和 DN,分别交 AB 于点 M,交 AC 于点 N(用尺规作图,不要求写作法,但保留作图痕迹);
(2)在(1)的条件下,判断直线 DM 与 DN 的位置关系.
名师导引 仿照教材 49 页的“作法”,但在第二步中,必须以大于第一步中两个交点之间线段长的一半为半径画弧.
(1)作∠ADB 和∠ADC 的平分线 DM 和 DN,分别交 AB 于点 M,交 AC 于点 N(用尺规作图,不要求写作法,但保留作图痕迹);
(2)在(1)的条件下,判断直线 DM 与 DN 的位置关系.

名师导引 仿照教材 49 页的“作法”,但在第二步中,必须以大于第一步中两个交点之间线段长的一半为半径画弧.
答案:
(1) 作图痕迹如下:
(以点 D 为顶点,分别作出∠ADB 和∠ADC 的平分线 DM、DN,交 AB 于 M,交 AC 于 N,保留尺规作图的弧线痕迹)
(2) DM ⊥ DN
证明:
∵ DM 平分∠ADB,DN 平分∠ADC,
∴ ∠ADM = ∠MDB = 1/2∠ADB,∠ADN = ∠NDC = 1/2∠ADC。
∵ 点 D 在 BC 上,
∴ ∠ADB + ∠ADC = 180°(平角定义)。
∴ ∠MDN = ∠ADM + ∠ADN = 1/2∠ADB + 1/2∠ADC = 1/2(∠ADB + ∠ADC) = 1/2×180° = 90°。
∴ DM ⊥ DN。
结论:直线 DM 与 DN 的位置关系是垂直。
(1) 作图痕迹如下:
(以点 D 为顶点,分别作出∠ADB 和∠ADC 的平分线 DM、DN,交 AB 于 M,交 AC 于 N,保留尺规作图的弧线痕迹)
(2) DM ⊥ DN
证明:
∵ DM 平分∠ADB,DN 平分∠ADC,
∴ ∠ADM = ∠MDB = 1/2∠ADB,∠ADN = ∠NDC = 1/2∠ADC。
∵ 点 D 在 BC 上,
∴ ∠ADB + ∠ADC = 180°(平角定义)。
∴ ∠MDN = ∠ADM + ∠ADN = 1/2∠ADB + 1/2∠ADC = 1/2(∠ADB + ∠ADC) = 1/2×180° = 90°。
∴ DM ⊥ DN。
结论:直线 DM 与 DN 的位置关系是垂直。
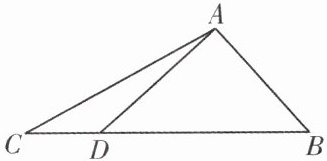
变式训练 如图,在钝角三角形 ABC 中,过钝角顶点 A 作 AD⊥AB 交 BC 于点 D.请用尺规作图法在 AB 边上求作一点 E,使得点 E 到 BC 的距离等于 AE 的长.(保留作图痕迹,不写作法)

答案:
作图步骤如下:
1. 以点D为圆心,适当长为半径画弧,分别交AD、BD于两点;
2. 分别以这两个交点为圆心,大于两交点间距离一半的长为半径画弧,在∠ADB内部交于一点;
3. 过点D和上述交点作射线,交AB于点E。
点E即为所求。
1. 以点D为圆心,适当长为半径画弧,分别交AD、BD于两点;
2. 分别以这两个交点为圆心,大于两交点间距离一半的长为半径画弧,在∠ADB内部交于一点;
3. 过点D和上述交点作射线,交AB于点E。
点E即为所求。
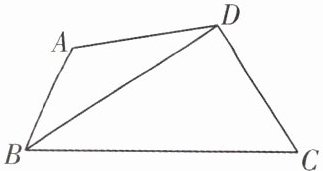
例 2 如图,在四边形 ABCD 中,BC > BA,BD 平分∠ABC,∠BAD + ∠C = 180°.求证:AD = CD.
名师导引 (1)有角的平分线(或证明是角的平分线)时,常过角平分线上的点向两边作垂线段,利用角平分线上的点到角的两边的距离相等证明结论;(2)有线段和、差关系时,常用截长法或补短法作辅助线,化和、差关系为相等关系.

名师导引 (1)有角的平分线(或证明是角的平分线)时,常过角平分线上的点向两边作垂线段,利用角平分线上的点到角的两边的距离相等证明结论;(2)有线段和、差关系时,常用截长法或补短法作辅助线,化和、差关系为相等关系.
答案:
证明:过点D作DE⊥BA交BA的延长线于点E,作DF⊥BC于点F。
∵BD平分∠ABC,DE⊥BA,DF⊥BC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°(平角定义),
∴∠EAD=∠C(同角的补角相等)。
在△AED和△CFD中,
∠EAD=∠C,
∠AED=∠CFD=90°,
DE=DF,
∴△AED≌△CFD(AAS)。
∴AD=CD(全等三角形的对应边相等)。
∵BD平分∠ABC,DE⊥BA,DF⊥BC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°(平角定义),
∴∠EAD=∠C(同角的补角相等)。
在△AED和△CFD中,
∠EAD=∠C,
∠AED=∠CFD=90°,
DE=DF,
∴△AED≌△CFD(AAS)。
∴AD=CD(全等三角形的对应边相等)。
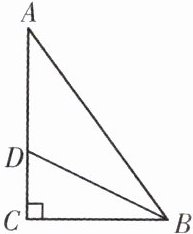
变式训练 如图,BD 是△ABC 的角平分线,∠C = 90°,CD = 3,△ABD 的面积是 15,则 AB 的长为
10
.
答案:
10
1. 两个完全相同的三角板如图摆放,它们的一组对应直角边分别在 AB,AC 上,且这组对应边所对的顶点重合于点 M,则点 M 一定在(

A.AC 边的高上
B.∠A 的平分线上
C.BC 边的中线上
D.∠B 的平分线上
B
)
A.AC 边的高上
B.∠A 的平分线上
C.BC 边的中线上
D.∠B 的平分线上
答案:
B
2. 如图,AD 是△ABC 的角平分线,AB = 8 cm,AC = 6 cm,则 $ S_{△ABD} : S_{△ACD} $ = (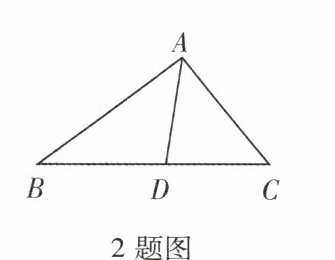
A.16 : 9
B.9 : 16
C.3 : 4
D.4 : 3
D
)
A.16 : 9
B.9 : 16
C.3 : 4
D.4 : 3
答案:
D
3. 如图,在 x 轴,y 轴上分别截取 OA,OB,使 OA = OB,再分别以点 A,B 为圆心,以大于 $\frac{1}{2}AB$ 的长度为半径画弧,两弧交于点 C.若 C 的坐标为(2a - 2,10 - a),则 a =
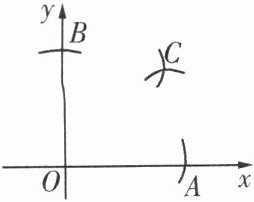
4
.
答案:
4
查看更多完整答案,请扫码查看


