第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
3. (2024·江苏南京·阶段练习)请仔细观察用尺规作一个角 $ \angle A ^ { \prime } O ^ { \prime } B ^ { \prime } $ 等于已知角 $ \angle AOB $ 的示意图,我们可以由 $ \triangle COD \cong \triangle C ^ { \prime } O ^ { \prime } D ^ { \prime } $ 得到 $ \angle A ^ { \prime } O ^ { \prime } B ^ { \prime } = \angle AOB $,请你写出 $ \triangle COD \cong \triangle C ^ { \prime } O ^ { \prime } D ^ { \prime } $ 的理由
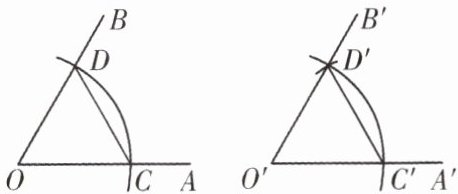
SSS
.
答案:
SSS
4. 如图,点 $ A $,$ B $,$ C $,$ D $ 在同一条直线上,$ AB = CD $,$ AE = DF $,$ CE = BF $. 求证:$ \triangle ACE \cong \triangle DBF $.
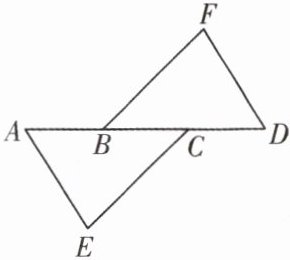

答案:
证明:
∵ 点A,B,C,D在同一条直线上,AB=CD,
∴ AB+BC=CD+BC,即AC=DB。
在△ACE和△DBF中,
∵ AE=DF,
AC=DB,
CE=BF,
∴ △ACE≌△DBF(SSS)。
∵ 点A,B,C,D在同一条直线上,AB=CD,
∴ AB+BC=CD+BC,即AC=DB。
在△ACE和△DBF中,
∵ AE=DF,
AC=DB,
CE=BF,
∴ △ACE≌△DBF(SSS)。
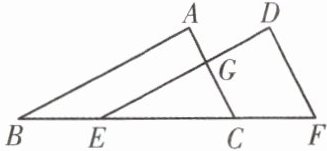
5. 如图,已知 $ E $,$ C $ 是线段 $ BF $ 上的点,满足 $ BE = CF $,$ A $,$ D $ 为线段上方两点,连接 $ AB $,$ AC $,$ DE $,$ DF $,满足 $ AB = DE $,$ AC = DF $.
(1)求证:$ \triangle ABC \cong \triangle DEF $;
(2)若五边形 $ ABFDG $ 的面积为 $ 16 $,$ \triangle GEC $ 的面积为 $ 4 $,请直接写出四边形 $ DGCF $ 的面积:
(1)求证:$ \triangle ABC \cong \triangle DEF $;
(2)若五边形 $ ABFDG $ 的面积为 $ 16 $,$ \triangle GEC $ 的面积为 $ 4 $,请直接写出四边形 $ DGCF $ 的面积:
6
.
(1)证明:
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SSS)。
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SSS)。
答案:
(1)证明:
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SSS)。
(2)6
(1)证明:
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$,
∴△ABC≌△DEF(SSS)。
(2)6
直角三角形全等的判定:斜边和
思考
对于两个直角三角形,除了直角相等,还需满足几个条件,这两个直角三角形就全等了?
练习
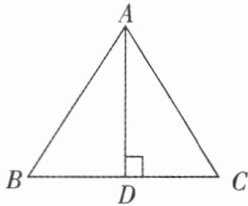
如图,△ABC中,AB = AC,AD是高,则△ADB与△ADC
一条直角边
分别相等的两个直角三角形全等. (可以简写成“斜边、直角边”或“HL”)思考
对于两个直角三角形,除了直角相等,还需满足几个条件,这两个直角三角形就全等了?
练习
如图,△ABC中,AB = AC,AD是高,则△ADB与△ADC
全等
(填“全等”或“不全等”). 根据是HL
.
答案:
一条直角边;全等;HL
探究一 利用“HL”证明直角三角形全等
例1 如图,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且BE = CF. 求证:∠B = ∠C.
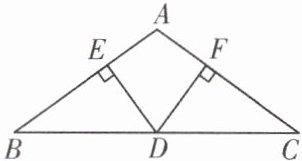
请补全下面的证明过程.
证明:∵ DE⊥AB,DF⊥AC,
∴ ∠BED =
∵ D是BC的中点,∴ BD =
又∵ BE = CF,
∴ Rt△BDE≌Rt△CDF
∴ ∠B = ∠C.
例1 如图,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且BE = CF. 求证:∠B = ∠C.

请补全下面的证明过程.
证明:∵ DE⊥AB,DF⊥AC,
∴ ∠BED =
∠CFD
= 90°.∵ D是BC的中点,∴ BD =
CD
.又∵ BE = CF,
∴ Rt△BDE≌Rt△CDF
HL
.∴ ∠B = ∠C.
答案:
∠CFD;CD;HL
查看更多完整答案,请扫码查看


