第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
例 2 如图,在 $ \triangle ABC $ 中, $ AB = AC $, $ AD $ 是 $ BC $ 边上的中线, $ BE \perp AC $ 于点 $ E $. 求证: $ \angle CBE = \frac{1}{2} \angle BAC $.


答案:
证明:
∵AB=AC,AD是BC边上的中线,
∴AD平分∠BAC,AD⊥BC(等腰三角形三线合一),
∴∠CAD=1/2∠BAC,∠ADC=90°,
∴∠C+∠CAD=90°.
∵BE⊥AC,
∴∠BEC=90°,
∴∠C+∠CBE=90°,
∴∠CBE=∠CAD(同角的余角相等),
∴∠CBE=1/2∠BAC.
∵AB=AC,AD是BC边上的中线,
∴AD平分∠BAC,AD⊥BC(等腰三角形三线合一),
∴∠CAD=1/2∠BAC,∠ADC=90°,
∴∠C+∠CAD=90°.
∵BE⊥AC,
∴∠BEC=90°,
∴∠C+∠CBE=90°,
∴∠CBE=∠CAD(同角的余角相等),
∴∠CBE=1/2∠BAC.
变式训练 如图,在 $ \triangle ABC $ 中, $ EF $ 是 $ AB $ 边的垂直平分线, $ AD \perp BC $ 于点 $ D $,且 $ D $ 为 $ CE $ 的中点.
(1) 求证: $ BE = AC $;
(2) 若 $ \angle C = 70^{\circ} $,求 $ \angle BAC $ 的度数.
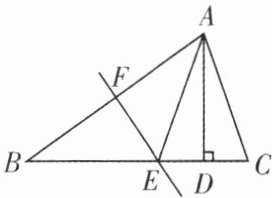
(1) 求证: $ BE = AC $;
(2) 若 $ \angle C = 70^{\circ} $,求 $ \angle BAC $ 的度数.

答案:
(1) 见解析;
(2) 75°
(1) 见解析;
(2) 75°
1. 如图,等腰 $ \triangle ABC $ 的顶角 $ \angle A $ 为 $ 40 $ 度,则它的底角 $ \angle B $ 为(
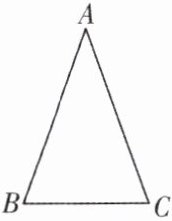
A.$ 70 $ 度
B.$ 60 $ 度
C.$ 50 $ 度
D.$ 40 $ 度
A
)
A.$ 70 $ 度
B.$ 60 $ 度
C.$ 50 $ 度
D.$ 40 $ 度
答案:
A
2. 如图 1 是两位同学玩跷跷板的场景,图 2 是跷跷板示意图,支柱 $ OC $ 与地面垂直,点 $ O $ 是 $ AB $ 的中点, $ AB $ 绕着点 $ O $ 上下转动. 若 $ A $ 端落地时, $ \angle OAC = 20^{\circ} $,则跷跷板上下可转动的最大角度(即 $ \angle A'OA $)是(
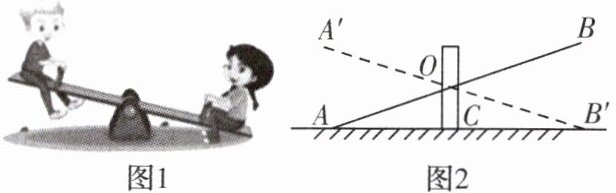
A.$ 30^{\circ} $
B.$ 50^{\circ} $
C.$ 40^{\circ} $
D.$ 70^{\circ} $
C
)
A.$ 30^{\circ} $
B.$ 50^{\circ} $
C.$ 40^{\circ} $
D.$ 70^{\circ} $
答案:
C
3. 将一台带有保护套的平板电脑按图 1 的方式放置在水平桌面上,其侧面示意图如图 2 所示. 经测量 $ AB = 10\,cm $, $ BC = 12\,cm $,若移动支点 $ A $ 的位置,使 $ \triangle ABC $ 是一个等腰三角形,则 $ \triangle ABC $ 的周长为
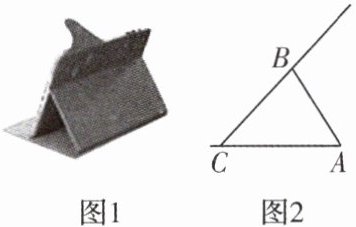
32cm或34cm
.
答案:
32cm或34cm
4. 等腰三角形在力学中也有应用. 如图,已知梁架 $ AG $ 与架底 $ AH $ 形成 $ 16^{\circ} $ 的夹角,为了分解 $ AG $ 的受力,现将长度相等的钢条焊接在上面,即 $ BC = CD = DE = EF $,又知 $ AB = BC $,这样可以使得梁架 $ AG $ 不易变形. 根据以上条件求得 $ \angle GEF = $
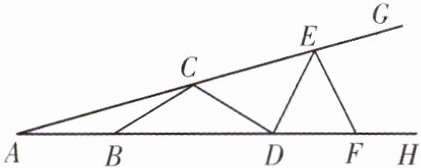
52
$^{\circ} $.
答案:
52
5. 如图,在 $ \triangle ABC $ 中, $ AB = AC $, $ D $ 是 $ BC $ 边的中点,连接 $ AD $,点 $ E $ 是 $ BC $ 延长线上一点, $ CF $ 平分 $ \angle ACE $,连接 $ AF $,且 $ AF = AC $.
(1) 若 $ \angle CAD = 31^{\circ} $,求 $ \angle B $ 的度数;
(2) 求证: $ AF // BE $.

(1) 若 $ \angle CAD = 31^{\circ} $,求 $ \angle B $ 的度数;
(2) 求证: $ AF // BE $.

答案:
(1)
∵AB=AC,D是BC中点,
∴AD平分∠BAC(等腰三角形三线合一)。
∵∠CAD=31°,
∴∠BAC=2∠CAD=62°。
∵AB=AC,
∴∠B=∠ACB。
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠B=(180°-∠BAC)/2=(180°-62°)/2=59°。
(2)
∵CF平分∠ACE,
∴∠ACF=∠ECF。
∵AF=AC,
∴∠ACF=∠AFC(等边对等角)。
∴∠AFC=∠ECF。
∴AF//BE(内错角相等,两直线平行)。
(1)
∵AB=AC,D是BC中点,
∴AD平分∠BAC(等腰三角形三线合一)。
∵∠CAD=31°,
∴∠BAC=2∠CAD=62°。
∵AB=AC,
∴∠B=∠ACB。
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠B=(180°-∠BAC)/2=(180°-62°)/2=59°。
(2)
∵CF平分∠ACE,
∴∠ACF=∠ECF。
∵AF=AC,
∴∠ACF=∠AFC(等边对等角)。
∴∠AFC=∠ECF。
∴AF//BE(内错角相等,两直线平行)。
查看更多完整答案,请扫码查看


