第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
变式训练 如图,若例2中$E,F分别为AB,CA$延长线上的点,仍有$BE= AF$,其他条件不变,那么$DE与DF$具有怎样的关系? 证明你的结论.
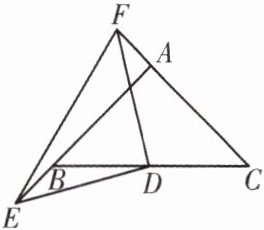

答案:
DE=DF且DE⊥DF.
证明:
∵△ABC是等腰三角形,AB=AC,D是BC中点(其他条件不变,隐含AB=AC,D为BC中点),
∴BD=CD,AD平分∠BAC,AD⊥BC(等腰三角形三线合一),∠ABC=∠ACB.
设∠ABC=∠ACB=β,则∠BAC=180°-2β,∠BAD=∠CAD=90°-β.
∵E在AB延长线上,F在CA延长线上,
∴∠EBD=180°-∠ABC=180°-β(平角定义),
∠FAD=180°-∠CAD=180°-(90°-β)=90°+β(平角定义).
又
∵∠BAC=180°-2β,∠FAB=∠ABC+∠ACB=2β(三角形外角性质),
∴∠FAD=∠FAB+∠BAD=2β+(90°-β)=90°+β,故∠EBD=∠FAD.
∵AD是等腰△ABC底边上的中线,
∴AD=BD(直角三角形斜边上的中线等于斜边一半,若∠BAC=90°,则AD=BD=CD).
又
∵BE=AF(已知),
∴△EBD≌△FAD(SAS),
∴DE=DF,∠EDB=∠FDA.
∵AD⊥BC,
∴∠ADB=90°,即∠EDB+∠ADE=90°.
∵∠EDB=∠FDA,
∴∠FDA+∠ADE=90°,即∠EDF=90°.
综上,DE=DF且DE⊥DF.
证明:
∵△ABC是等腰三角形,AB=AC,D是BC中点(其他条件不变,隐含AB=AC,D为BC中点),
∴BD=CD,AD平分∠BAC,AD⊥BC(等腰三角形三线合一),∠ABC=∠ACB.
设∠ABC=∠ACB=β,则∠BAC=180°-2β,∠BAD=∠CAD=90°-β.
∵E在AB延长线上,F在CA延长线上,
∴∠EBD=180°-∠ABC=180°-β(平角定义),
∠FAD=180°-∠CAD=180°-(90°-β)=90°+β(平角定义).
又
∵∠BAC=180°-2β,∠FAB=∠ABC+∠ACB=2β(三角形外角性质),
∴∠FAD=∠FAB+∠BAD=2β+(90°-β)=90°+β,故∠EBD=∠FAD.
∵AD是等腰△ABC底边上的中线,
∴AD=BD(直角三角形斜边上的中线等于斜边一半,若∠BAC=90°,则AD=BD=CD).
又
∵BE=AF(已知),
∴△EBD≌△FAD(SAS),
∴DE=DF,∠EDB=∠FDA.
∵AD⊥BC,
∴∠ADB=90°,即∠EDB+∠ADE=90°.
∵∠EDB=∠FDA,
∴∠FDA+∠ADE=90°,即∠EDF=90°.
综上,DE=DF且DE⊥DF.
1. 根据下列条件,不能判断$\triangle ABC$是等腰三角形的是(
A.$∠A:∠B:∠C= 2:2:5$
B.$a:b:c= 3:3:4$
C.$∠A= 30^{\circ },∠C= 120^{\circ }$
D.$2∠A= ∠B+∠C$
D
)A.$∠A:∠B:∠C= 2:2:5$
B.$a:b:c= 3:3:4$
C.$∠A= 30^{\circ },∠C= 120^{\circ }$
D.$2∠A= ∠B+∠C$
答案:
D
2. 在平面直角坐标系中,已知$A(3,0)$,$B(0,3)$,若点$C$在坐标轴上,且$\triangle ABC$为等腰三角形,则满足条件的点$C$的个数是(
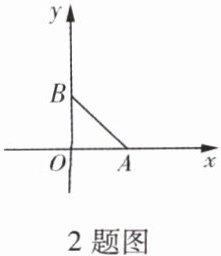
A.3
B.4
C.6
D.7
D
)
A.3
B.4
C.6
D.7
答案:
D
3. 如图,在$\triangle ABC$中,$ED// BC$,$∠ABC和∠ACB的平分线分别交ED于点G,F$,若$FG= 4$,$ED= 8$,则$EB+DC= $
4
.
答案:
4
4. 如图,在$\triangle ABC的BC边上截取BE= AB$,连接$AE$,作$∠ABE的角平分线BD交AE于点D$,若$∠EAC= ∠C$,$BC= 17$,$AB= 9$,则$AD= $
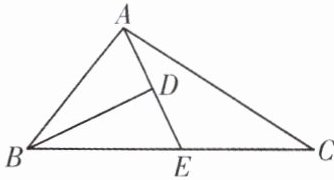
4
.
答案:
4
5. 如图,在$\triangle ABC$中,$AC= BC$,$∠ACB= 84^{\circ }$,$D是AB$边上一点(不与$A,B$重合),以$CD为边作等腰\triangle CDE$,$CD= CE$,且$∠DCE= 84^{\circ }$,$CB与DE交于点F$,连接$BE$.
(1)求证:$\triangle ACD\cong \triangle BCE$;
(2)当$AD= BF$时,证明$\triangle DCF$是等腰三角形.
(1)求证:$\triangle ACD\cong \triangle BCE$;
(2)当$AD= BF$时,证明$\triangle DCF$是等腰三角形.

答案:
(1)证明:
∵AC=BC,CD=CE,∠ACB=∠DCE=84°,
∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE。在△ACD和△BCE中,$\left\{\begin{array}{l}AC=BC\\ \angle ACD=\angle BCE\\ CD=CE\end{array}\right.$,
∴△ACD≌△BCE(SAS)。
(2)证明:
∵AC=BC,∠ACB=84°,
∴∠A=∠ABC=$\frac{180^{\circ}-84^{\circ}}{2}=48^{\circ}$。由
(1)知△ACD≌△BCE,
∴AD=BE,∠A=∠CBE=48°。
∵AD=BF,
∴BE=BF,
∴△BEF中,∠BEF=∠BFE=$\frac{180^{\circ}-\angle CBE}{2}=\frac{180^{\circ}-48^{\circ}}{2}=66^{\circ}$。
∵∠BFE=∠DFC,
∴∠DFC=66°。
∵CD=CE,∠DCE=84°,
∴∠CDE=$\frac{180^{\circ}-84^{\circ}}{2}=48^{\circ}$。在△DCF中,∠DCF=180°-∠CDE-∠DFC=180°-48°-66°=66°。
∴∠DCF=∠DFC,
∴DF=DC,即△DCF是等腰三角形。
(1)证明:
∵AC=BC,CD=CE,∠ACB=∠DCE=84°,
∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE。在△ACD和△BCE中,$\left\{\begin{array}{l}AC=BC\\ \angle ACD=\angle BCE\\ CD=CE\end{array}\right.$,
∴△ACD≌△BCE(SAS)。
(2)证明:
∵AC=BC,∠ACB=84°,
∴∠A=∠ABC=$\frac{180^{\circ}-84^{\circ}}{2}=48^{\circ}$。由
(1)知△ACD≌△BCE,
∴AD=BE,∠A=∠CBE=48°。
∵AD=BF,
∴BE=BF,
∴△BEF中,∠BEF=∠BFE=$\frac{180^{\circ}-\angle CBE}{2}=\frac{180^{\circ}-48^{\circ}}{2}=66^{\circ}$。
∵∠BFE=∠DFC,
∴∠DFC=66°。
∵CD=CE,∠DCE=84°,
∴∠CDE=$\frac{180^{\circ}-84^{\circ}}{2}=48^{\circ}$。在△DCF中,∠DCF=180°-∠CDE-∠DFC=180°-48°-66°=66°。
∴∠DCF=∠DFC,
∴DF=DC,即△DCF是等腰三角形。
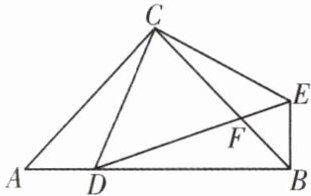
6. 如图,$\triangle ABC和\triangle CDE$均为等腰三角形,$AC= BC$,$EC= DC$,$A,E,D$三点共线,$BD⊥AD于点D$,$AD交BC于点F$.
(1)若$∠ACE= ∠BCD$,$AD= 8$,$BD= \frac {2}{5}AD$,求$DE$的长;
(2)若$∠ACB= ∠ECD= 90^{\circ }$,且$BD= CE$,求证:$BC= AB - CF$.
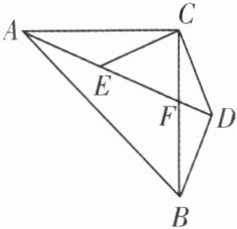
(1)若$∠ACE= ∠BCD$,$AD= 8$,$BD= \frac {2}{5}AD$,求$DE$的长;
(2)若$∠ACB= ∠ECD= 90^{\circ }$,且$BD= CE$,求证:$BC= AB - CF$.

答案:
(1)$\frac{24}{5}$;
(2)证明见上
(1)$\frac{24}{5}$;
(2)证明见上
查看更多完整答案,请扫码查看


