第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1.(数学与生活)如图是某公园一段索道的示意图,已知 $A$,$B$ 分别为索道的起点和终点,且 $A$,$B$ 两点间的距离 $AB$ 为 $40$ 米,$\angle BAC = 30^{\circ}$,则缆车从 $A$ 点到 $B$ 点的高程($BC$ 的长)为(
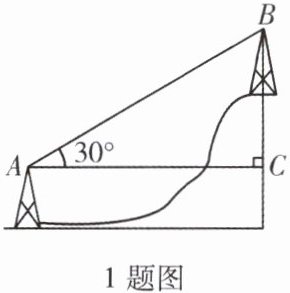
A.$20$ 米
B.$17.5$ 米
C.$15$ 米
D.$12.5$ 米
A
)
A.$20$ 米
B.$17.5$ 米
C.$15$ 米
D.$12.5$ 米
答案:
A
2. 如图,$OP$ 平分 $\angle AOB$,$\angle AOB = 60^{\circ}$,$PD\perp OA$ 于点 $D$,$E$ 是射线 $OB$ 上的一个动点,若 $OP = 6$,则 $PE$ 的最小值为(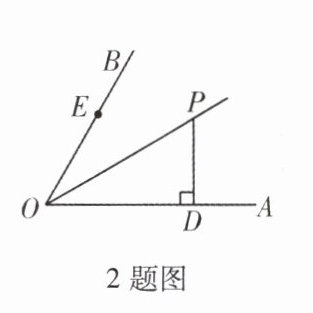
A.$2$
B.$3$
C.$4$
D.$5$
B
)
A.$2$
B.$3$
C.$4$
D.$5$
答案:
B
3. 如图是某商场一楼与二楼之间的手扶电梯示意图。其中 $AB$、$CD$ 分别表示一楼、二楼地面的水平线,$\angle ABC = 150^{\circ}$,$BC$ 的长是 $10\ m$,则乘电梯从点 $B$ 到点 $C$ 上升的高度 $h$ 是
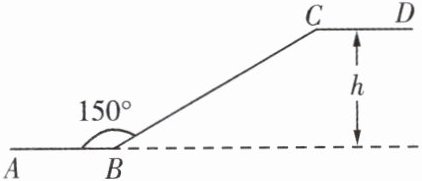
5
$m$。
答案:
5
4. 在等腰 $\triangle ABC$ 中,$AB = AC = 4$,$\angle BAC = 30^{\circ}$,$D$ 在 $BC$ 边上,$DE\perp AB$ 于 $E$,$DF\perp AC$ 于 $F$,则 $DE + DF = $
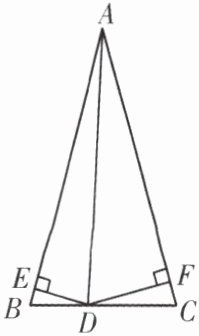
2
。
答案:
2
5.(操作探究)教材利用倍长 $BC$ 的方法发现了结论:“在直角三角形中,如果有一个锐角等于 $30^{\circ}$,那么它所对的直角边等于斜边的一半。”我们还能用其他的方法证明这个结论吗?
下面是小明的探究过程,请根据他的思路完成以下作图和填空:
如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,求证:$AC = \frac{1}{2}AB$。
(1) 尺规作图:作 $\angle CAB$ 的角平分线交 $BC$ 于点 $D$,在 $AB$ 上取一点 $E$,使得 $AE = AC$,连接 $DE$(保留作图痕迹,不写作法);
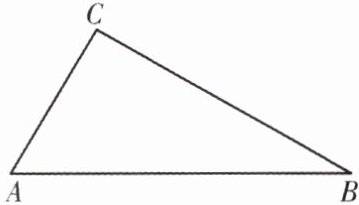
(2) 证明:$\because \angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,
$\therefore \angle CAB = $
$\because AD$ 平分 $\angle CAB$,
$\therefore \angle CAD = $
在 $\triangle ACD$ 与 $\triangle AED$ 中,
$\begin{cases}AC = AE, \\\angle CAD = \angle EAD, \\AD = AD,\end{cases} $
$\therefore \triangle ACD\cong \triangle AED(SAS)$,
$\therefore$
$\therefore DE\perp AB$。
又 $\because \angle ABC = \angle EAD = 30^{\circ}$,
$\therefore DA = $
$\therefore$ 点 $E$ 是 $AB$ 的中点。
$\therefore$
$\because AC = AE$,
$\therefore AC = \frac{1}{2}AB$。
下面是小明的探究过程,请根据他的思路完成以下作图和填空:
如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,求证:$AC = \frac{1}{2}AB$。
(1) 尺规作图:作 $\angle CAB$ 的角平分线交 $BC$ 于点 $D$,在 $AB$ 上取一点 $E$,使得 $AE = AC$,连接 $DE$(保留作图痕迹,不写作法);

(2) 证明:$\because \angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,
$\therefore \angle CAB = $
60°
,$\because AD$ 平分 $\angle CAB$,
$\therefore \angle CAD = $
∠EAD
$= 30^{\circ}$。在 $\triangle ACD$ 与 $\triangle AED$ 中,
$\begin{cases}AC = AE, \\\angle CAD = \angle EAD, \\AD = AD,\end{cases} $
$\therefore \triangle ACD\cong \triangle AED(SAS)$,
$\therefore$
∠AED
$= \angle ACB = 90^{\circ}$,$\therefore DE\perp AB$。
又 $\because \angle ABC = \angle EAD = 30^{\circ}$,
$\therefore DA = $
DB
,$\therefore$ 点 $E$ 是 $AB$ 的中点。
$\therefore$
AE
$= \frac{1}{2}AB$。$\because AC = AE$,
$\therefore AC = \frac{1}{2}AB$。
答案:
(1) (作图痕迹略,需作出∠CAB的角平分线AD交BC于D,在AB上截取AE=AC,连接DE)
(2) 60°;∠EAD;∠AED;DB;AE
(1) (作图痕迹略,需作出∠CAB的角平分线AD交BC于D,在AB上截取AE=AC,连接DE)
(2) 60°;∠EAD;∠AED;DB;AE
查看更多完整答案,请扫码查看


