《2025年学习指要八年级数学上册人教版》

3. 如图,在$\triangle ABC$中,$∠BAC = 90^{\circ}$,$AD⊥BC$,$∠B = 31^{\circ}$,则$∠DAC = $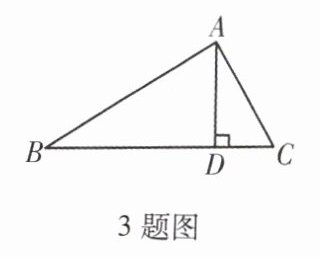31$^{\circ}$.

答案： $31$

4. 如图,$∠C = 90^{\circ}$,$∠1 = ∠2$,$\triangle ADE$是直角三角形吗? 为什么?

答案： △ADE是直角三角形，理由如下：
∵∠C=90°，
∴∠A+∠B=90°。
∵∠1=∠2，
∴∠AED=∠1+∠C=∠2+90°（此处修正：应为∠AED=∠1+∠C，而∠C=90°，所以∠AED=∠1+90°，但根据三角形内角和，在△ADE中，∠A+∠AED+∠ADE=180°，又因为∠ADE=∠2（对顶角相等），所以∠A+∠1+90°+∠2=180°，又∠1=∠2，∠A+∠B=90°且∠B=∠2（原条件∠1=∠2，图中∠B应为∠2），所以∠A+∠2=90°，代入得90°+90°=180°，即∠AED=90°，所以△ADE是直角三角形。）
（注：原解答过程中“∠AED=∠2+90°”表述不准确，修正后通过对顶角和三角形内角和推导得出∠AED=90°，从而证明△ADE是直角三角形。）
最终规范解答：
△ADE是直角三角形。
理由：
∵∠C=90°，
∴∠A+∠B=90°。
∵∠1=∠2，∠ADE=∠2（对顶角相等），
∴∠ADE=∠1。
在△AED中，∠A+∠1+∠AED=180°，
又∠A+∠B=90°，∠B=∠2=∠1，
∴∠A+∠1=90°，
∴90°+∠AED=180°，
∴∠AED=90°，
∴△ADE是直角三角形。

5. 如图1,在$\triangle ABC$中,$AD⊥BC于点D$,$CE⊥AB于点E$.


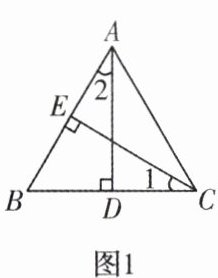
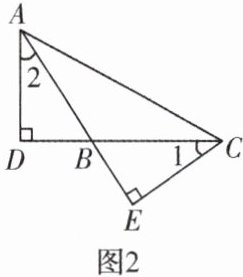
(1)猜测$∠1与∠2$的关系,说明理由;
(2)如图2,如果$∠ABC$是钝角,其余条件不变,(1)中的结论是否仍然成立? 请说明理由.

答案：
(1)∠1=∠2.
理由：
∵AD⊥BC，CE⊥AB，
∴∠ADB=∠CEB=90°.
在Rt△ABD中，∠2+∠B=90°；在Rt△CBE中，∠1+∠B=90°.
∴∠1=∠2（同角的余角相等）.
(2)结论仍然成立，∠1=∠2.
理由：
∵AD⊥BC，CE⊥AB，
∴∠ADB=∠CEB=90°.
∵∠ABC是钝角，
∴∠ABD=∠CBE=180°-∠ABC.
在Rt△ABD中，∠2+∠ABD=90°，则∠2=90°-∠ABD=90°-(180°-∠ABC)=∠ABC-90°.
在Rt△CBE中，∠1+∠CBE=90°，则∠1=90°-∠CBE=90°-(180°-∠ABC)=∠ABC-90°.
∴∠1=∠2.

6. 如图,$\triangle ABC$中,$∠ACB = 90^{\circ}$,$∠1 = ∠B$.
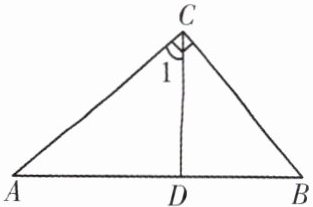
(1)试说明$CD是\triangle ABC$的高;
(2)如果$AC = 8$,$BC = 6$,$AB = 10$,求$CD$的长.

答案：
(1) 因为∠ACB=90°，所以∠1+∠BCD=90°。又因为∠1=∠B，所以∠B+∠BCD=90°。在△BCD中，∠BDC=180°-(∠B+∠BCD)=180°-90°=90°，即CD⊥AB，所以CD是△ABC的高。
(2) 由三角形面积公式，S△ABC=1/2×AC×BC=1/2×AB×CD。已知AC=8，BC=6，AB=10，代入得1/2×8×6=1/2×10×CD，解得CD=4.8。

三角形外角的性质：
性质一：三角形的外角等于与它不相邻的两个内角的和；
性质二：三角形的外角大于任何一个与它不相邻的内角。
思考 你能证明三角形外角的性质一、二吗？有哪些方法？
练习(1)若三角形的外角中有一个是锐角,则这个三角形是钝角三角形。
(2)△ABC 中,若∠C - ∠B = ∠A,则△ABC 的外角中最小的角是直角。(填“锐角”“直角”或“钝角”)

答案： 等于；大于；钝角；直角

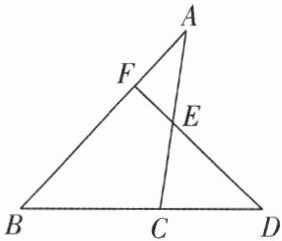
例 1 如图,已知 D 是△ABC 的边 BC 延长线上一点,DF 交 AC 于点 E,∠A = 35°,∠ACD = 83°。
(1)求∠B 的度数；
(2)若∠D = 42°,求∠AFE 的度数。

(1)$48^{\circ}$；(2)$90^{\circ}$；
变式训练(跨学科融合)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心 O 的光线相交于点 P,点 F 为凸透镜的焦点。若∠1 = 155°,∠2 = 30°,则∠3 的度数为(C)

A. 45° B. 50° C. 55° D. 60°

答案： 例1
(1)$48^{\circ}$；
(2)$90^{\circ}$；变式训练C。