第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
变式训练 如图,在△ABC中,DE是AB的垂直平分线,交AB于点D,交BC于点E,连接AE,已知BD= 2 cm,△ACE的周长为6 cm,则△ABC的周长为
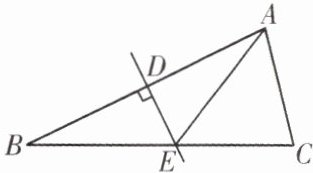
10
cm.
答案:
∵DE是AB的垂直平分线,
∴AD=BD=2cm,AE=BE。
∵BD=2cm,
∴AB=AD+BD=2+2=4cm。
∵△ACE的周长为6cm,
∴AE+EC+AC=6cm。
∵AE=BE,
∴BE+EC+AC=BC+AC=6cm。
∴△ABC的周长=AB+BC+AC=4+6=10cm。
10
∵DE是AB的垂直平分线,
∴AD=BD=2cm,AE=BE。
∵BD=2cm,
∴AB=AD+BD=2+2=4cm。
∵△ACE的周长为6cm,
∴AE+EC+AC=6cm。
∵AE=BE,
∴BE+EC+AC=BC+AC=6cm。
∴△ABC的周长=AB+BC+AC=4+6=10cm。
10
探究二 线段的垂直平分线的判定的应用
例2 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F.
求证:AD垂直平分EF.
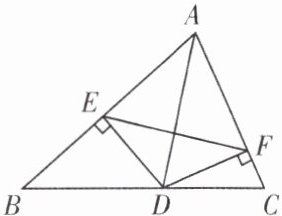
名师导引 本题只要证得AE= AF,DE= DF,根据垂直平分线的判定方法,以及两点确定一条直线,即可迎刃而解.
例2 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F.
求证:AD垂直平分EF.

名师导引 本题只要证得AE= AF,DE= DF,根据垂直平分线的判定方法,以及两点确定一条直线,即可迎刃而解.
答案:
证明:
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF(角的平分线上的点到角的两边的距离相等),
∴点D在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
在Rt△AED和Rt△AFD中,
∵AD=AD,DE=DF,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
∵点A、D都在线段EF的垂直平分线上,
∴AD垂直平分EF(两点确定一条直线)。
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF(角的平分线上的点到角的两边的距离相等),
∴点D在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
在Rt△AED和Rt△AFD中,
∵AD=AD,DE=DF,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
∵点A、D都在线段EF的垂直平分线上,
∴AD垂直平分EF(两点确定一条直线)。
变式训练 如图,AD与BC相交于点O,AB= CD,∠ABC= ∠CDA,EB= ED,连接OE,BD.求证:OE垂直平分BD.
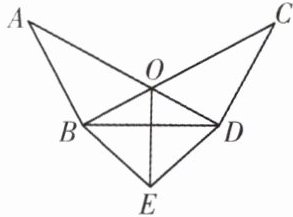

答案:
在△ABO 和△CDO 中,
$\begin{cases}\angle ABC = \angle CDA, \\\angle AOB = \angle COD(对顶角相等), \\AB = CD.\end{cases}$
根据$AAS$(角角边)判定,得$\triangle ABO \cong \triangle CDO$,
根据全等三角形的性质,对应边相等,所以$OB = OD$,
即点O在线段BD的垂直平分线上。
因为$EB = ED$,
根据线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,
所以点E也在线段BD的垂直平分线上。
因为两点确定一条直线,
所以直线OE就是线段BD的垂直平分线,
即$OE$垂直平分$BD$。
$\begin{cases}\angle ABC = \angle CDA, \\\angle AOB = \angle COD(对顶角相等), \\AB = CD.\end{cases}$
根据$AAS$(角角边)判定,得$\triangle ABO \cong \triangle CDO$,
根据全等三角形的性质,对应边相等,所以$OB = OD$,
即点O在线段BD的垂直平分线上。
因为$EB = ED$,
根据线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,
所以点E也在线段BD的垂直平分线上。
因为两点确定一条直线,
所以直线OE就是线段BD的垂直平分线,
即$OE$垂直平分$BD$。
1. 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD,若BC= 9 cm,BD= 4 cm,则AD的长为(
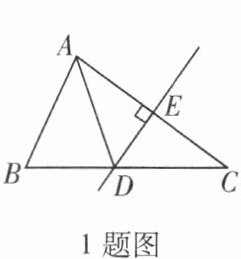
A.3 cm
B.4 cm
C.5 cm
D.9 cm
C
)
A.3 cm
B.4 cm
C.5 cm
D.9 cm
答案:
C
2. 如图是“一带一路”示意图,记北京为A地,莫斯科为B地,雅典为C地.若想建立一个货物中转仓,使其到A,B,C三地的距离相等,则中转仓的位置应选在(
A.三边垂直平分线的交点
B.三边中线的交点
C.三条角平分线的交点
D.三边上高的交点
A
)
A.三边垂直平分线的交点
B.三边中线的交点
C.三条角平分线的交点
D.三边上高的交点
答案:
A
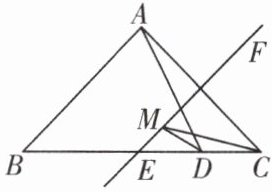
3. 如图,在△ABC中,点D在BC边上,连接AD,CD= 5,AD= 13,直线EF是边AC的垂直平分线,点M在直线EF上运动,连接DM,CM,△CDM周长的最小值为(
A.8
B.16
C.18
D.20
C
)
A.8
B.16
C.18
D.20
答案:
C
查看更多完整答案,请扫码查看


