第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
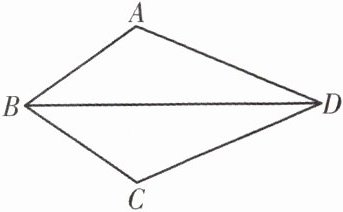
4. (2024·广东广州·二模)古人诗云:“草长莺飞二月天,拂堤杨柳醉春烟. 儿童散学归来早,忙趁东风放纸鸢.”纸鸢,又称风筝,其制作技艺是我国民间的传统工艺. 某班数学兴趣小组根据风筝的形状画出图形(如图所示),已知$AB = BC$,$\angle ABD = \angle CBD$,求证:$AD = CD$.

答案:
在$\triangle ABD$和$\triangle CBD$中,
$\left\{ \begin{matrix} AB = BC, \\\angle ABD = \angle CBD, \\BD = BD. \end{matrix} \right.$
根据$SAS$(边角边)全等判定定理得:
$\triangle ABD ≌ \triangle CBD$。
所以$AD = CD$。
$\left\{ \begin{matrix} AB = BC, \\\angle ABD = \angle CBD, \\BD = BD. \end{matrix} \right.$
根据$SAS$(边角边)全等判定定理得:
$\triangle ABD ≌ \triangle CBD$。
所以$AD = CD$。
5. (23 - 24 四川泸州·阶段练习,有改编)倍长中线法与作平行线是构造全等三角形常见的作辅助线的方法.
(1)如图 1,在$\triangle ABC$中,$AC = 5$,中线$AD = 6$,求$AB$的取值范围. 方法一:延长$AD到E使DE = AD$,连接$CE$;方法二:过点$C作AB的平行线交AD的延长线于E$. 请你从以上两种方法中选一种方法证明$\triangle ECD\cong\triangle ABD$,并直接写出$AB$的取值范围.
(2)如图 2,在$\triangle AEC$中,点$B$,$D在EC$上,$AE = 2AD$,点$D是BC$的中点,若$AB平分\angle DAE$,求证:$AC = BE$.

(1)如图 1,在$\triangle ABC$中,$AC = 5$,中线$AD = 6$,求$AB$的取值范围. 方法一:延长$AD到E使DE = AD$,连接$CE$;方法二:过点$C作AB的平行线交AD的延长线于E$. 请你从以上两种方法中选一种方法证明$\triangle ECD\cong\triangle ABD$,并直接写出$AB$的取值范围.
(2)如图 2,在$\triangle AEC$中,点$B$,$D在EC$上,$AE = 2AD$,点$D是BC$的中点,若$AB平分\angle DAE$,求证:$AC = BE$.

答案:
(1)7<AB<17;
(2)证明见上。
(1)7<AB<17;
(2)证明见上。
三角形全等的判定:
三角形全等的判定:
思考 有两角及一边分别对应相等的两个三角形全等吗?
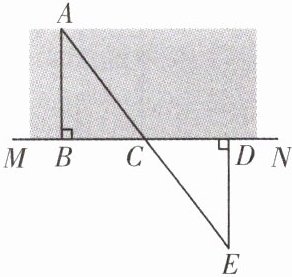
练习 在数学综合实践活动课上,张老师给了各活动小组大直角三角尺一个、皮尺一条,测量如图所示小河的宽度(A 为河岸边的一棵柳树).小颖是这样做的:①在 A 点的对岸作直线 MN;②用三角尺作 AB⊥MN,垂足为 B;③在直线 MN 上另取两点 C,D,使 BC = CD;④过点 D 作 DE⊥MN 交 AC 的延长线于点 E,由三角形全等可知 DE 的长度等于河宽 AB.
在以上做法中,△ABC≌△EDC 的依据是
两角和它们的夹边分别相等的两个三角形全等
.(可以简写成“角边角”或“ASA”)三角形全等的判定:
两角和其中一角的对边分别相等的两个三角形全等
.(可以简写成“角角边”或“AAS”)思考 有两角及一边分别对应相等的两个三角形全等吗?
有
练习 在数学综合实践活动课上,张老师给了各活动小组大直角三角尺一个、皮尺一条,测量如图所示小河的宽度(A 为河岸边的一棵柳树).小颖是这样做的:①在 A 点的对岸作直线 MN;②用三角尺作 AB⊥MN,垂足为 B;③在直线 MN 上另取两点 C,D,使 BC = CD;④过点 D 作 DE⊥MN 交 AC 的延长线于点 E,由三角形全等可知 DE 的长度等于河宽 AB.
在以上做法中,△ABC≌△EDC 的依据是
ASA
.
答案:
两角和它们的夹边分别相等的两个三角形全等;两角和其中一角的对边分别相等的两个三角形全等;有;ASA
查看更多完整答案,请扫码查看


