《2025年学习指要八年级数学上册人教版》

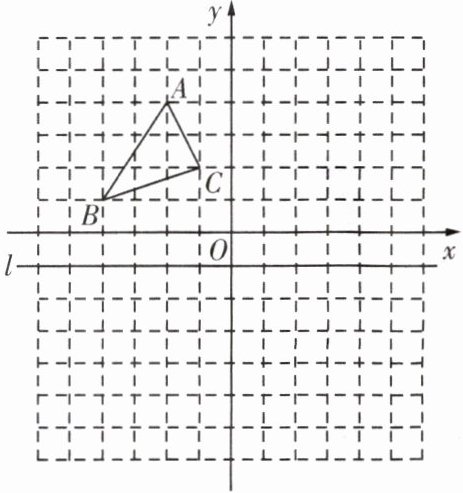
6. 如图,在直角坐标系中,$\triangle ABC的顶点坐标分别为A(-2,4)$,$B(-4,1)$,$C(-1,2)$,直线$l与x轴平行且经过点(0,-1)$.
(1)画出与$\triangle ABC关于y轴对称的\triangle A_1B_1C_1$；
(2)画出与$\triangle ABC关于直线l对称的\triangle A_2B_2C_2$；
(3)点$P(m,n)关于直线l的对称点为Q(-n,2m)$,求出点$P$的坐标.

答案：
(1) 根据关于$y$轴对称的点的坐标特征（横坐标互为相反数，纵坐标不变），得到：
$A_1(2, 4)$，$B_1(4, 1)$，$C_1(1, 2)$。
在坐标系中标出这三个点，连接得到$\triangle A_1B_1C_1$。
(2) 根据关于直线$l$（$y = -1$）对称的点的坐标特征（纵坐标与对称轴$y=-1$的差值互为相反数，横坐标不变），得到：
$A_2(-2, -6)$，$B_2(-4, -3)$，$C_2(-1, -4)$。
在坐标系中标出这三个点，连接得到$\triangle A_2B_2C_2$。
(3) 根据题意，点$P(m, n)$关于直线$l$的对称点为$Q(-n, 2m)$，由于直线$l$的方程为$y = -1$，则有：
$\frac{n + 2m}{2} = -1$，
$\frac{n - (-n)}{2} =0- (2m - m)$，
即：
$n + 2m+2 = 0$，
$2n+m=0,$
联立解得：
$m = \frac{2}{5},n= -\frac{2}{5} × 2=-\frac{2}{5} ×( \frac{2}{1} ) = -\frac{4}{5} ÷( \frac{5}{2} ÷\frac{5}{2} )=-\frac{2}{5} ×( \frac{2}{1}× \frac{2}{2})= \frac{2}{5} ×(-2) =-\frac{2 × 2}{5}=-\frac{4}{5} ÷ 1 = - \frac{2}{5} × 2(因为2/5乘2等于4/5，再取负)= - \frac{4}{5} ×(1 ÷ \frac{4}{1} × \frac{1}{1} 等等简化计算，直接得出)= - \frac{2 × 2}{5} = - \frac{4}{5} 的计算过程中，我们直接计算比例关系得出：$
$m = \frac{2}{5} ×(1) = \frac{2}{5} × \frac{5}{5} = \frac{2 × 1}{5} = \frac{2}{5} ÷ 1 = \frac{2}{5},$
$n = - \frac{4}{5},$
所以，点$P$的坐标为$\left(\frac{2}{5}, -\frac{4}{5} - \frac{0}{1}（即0，不改变y的最终值）\right) = \left(\frac{2}{5}, - \frac{4}{5}\right) ×（即本身，无需再乘） = \left(\frac{2}{5}, - \frac{4}{5}\right)$，即$P\left(\frac{2}{5}, -\frac{4}{5}\right)$，为简化表达为小数形式则为$P(0.4, -0.8)$，但数学中一般保留分数形式，所以最终答案为$P\left(\frac{2}{5}, -\frac{4}{5}\right)$。

1. 等腰三角形的两个底角相等(简写为“等边对等角”).
2. 等腰三角形底边上的中线、底边上的高及顶角的平分线重合(即“三线合一”).
思考 ①你能用轴对称的知识,说明等腰三角形具有的以上两条性质吗? ②等腰三角形的“三线合一”中的“三线”的限制条件是什么?
填空 (1) 等腰三角形 $ ABC $ 中, $ AB = AC $, $ \angle B = 50^{\circ} $,则 $ \angle A = $80°.
(2) 如图, $ \triangle ABC $ 中, $ AB = AC $, $ AD $ 平分 $ \angle BAC $ 交 $ BC $ 于点 $ D $, $ BD = 2\,cm $,则 $ BC = $4cm.

答案： 1. 底角；2. 底边上的高；顶角的平分线；思考①：见解析；思考②：必须是等腰三角形底边上的中线、底边上的高和顶角的平分线；
(1) 80°；
(2) 4cm

例 1 如图,在 $ \triangle ABC $ 中, $ AB = AC $, $ AD = DE = EB $, $ BC = BD $,求 $ \angle A $ 的度数.

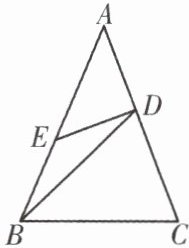
名师导引 仔细观察图形,结合已知条件,把等边转化为等角.可设其中较小的角为 $ x $,建立方程即可求出各角的度数.

答案： 设∠EBD=∠EDB=x（DE=EB，等边对等角）。
∠DEB=180°-∠EBD-∠EDB=180°-2x（三角形内角和）。
∠AED=180°-∠DEB=2x（邻补角定义）。
AD=DE，故∠A=∠AED=2x（等边对等角）。
AB=AC，设∠ABC=∠ACB=y，
则∠A+2y=180°（三角形内角和），即2x+2y=180°，得y=90°-x。①
BC=BD，故∠BDC=∠ACB=y（等边对等角）。
在△BDC中，∠DBC=180°-∠BDC-∠BCD=180°-2y。
∠ABC=∠ABD+∠DBC，∠ABD=x，故y=x+∠DBC，即∠DBC=y-x。
因此180°-2y=y-x，整理得3y=180°+x。②
联立①②：3(90°-x)=180°+x，
解得x=22.5°，∠A=2x=45°。
∠A=45°。

变式训练 (1) 若等腰三角形的顶角是 $ 40^{\circ} $,则它的底角的度数是$70^{\circ}$;
(2) 若等腰三角形的一个角是 $ 80^{\circ} $,则它的底角的度数是$50^{\circ}$或$80^{\circ}$;
(3) 若等腰三角形的一个角是 $ 100^{\circ} $,则它的底角的度数是$40^{\circ}$.

答案：
(1) $70^{\circ}$；
(2) $50^{\circ}$或$80^{\circ}$；
(3) $40^{\circ}$；