第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
例2 如图,$\triangle ABC\cong\triangle DEB$,$AB= DE$。若$\angle A= 100^{\circ}$,$BC= 8$,则$\angle BDE= $
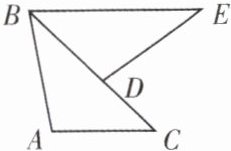
名师导引 利用全等三角形的性质既可以直接确定对应边或对应角的相等关系,又可以求解相关线段的长度或相关角的大小。
100°
,$BE= $8
。
名师导引 利用全等三角形的性质既可以直接确定对应边或对应角的相等关系,又可以求解相关线段的长度或相关角的大小。
答案:
100°,8
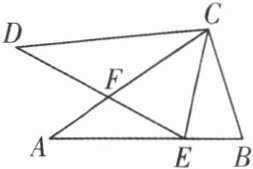
变式训练 如图,$\triangle ABC\cong\triangle DEC$,点$E在AB$上,$AC与DE相交于点F$,$BC= 6$,$BE= 3$。求$\triangle EBC$的周长。

答案:
解:
∵△ABC≌△DEC,
∴BC=EC=6。
∵BE=3,
∴△EBC的周长=EB+BC+EC=3+6+6=15。
答:△EBC的周长为15。
∵△ABC≌△DEC,
∴BC=EC=6。
∵BE=3,
∴△EBC的周长=EB+BC+EC=3+6+6=15。
答:△EBC的周长为15。
1. 在下列各组图形中,不是全等图形的是(
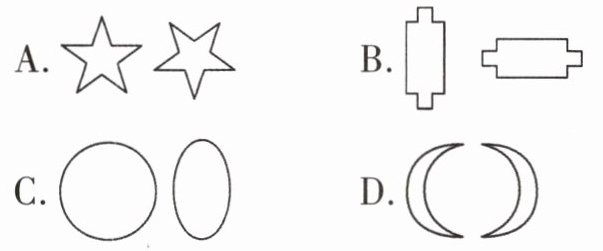
C
)
答案:
C
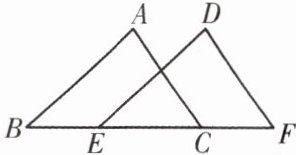
2. 如图,$\triangle ABC\cong\triangle DEF$,$A与D$,$B与E$分别是对应顶点,且测得$BC= 5\mathrm{cm}$,$BF= 7\mathrm{cm}$,则$EC$长为(
A.$1\mathrm{cm}$
B.$2\mathrm{cm}$
C.$3\mathrm{cm}$
D.$4\mathrm{cm}$
C
)
A.$1\mathrm{cm}$
B.$2\mathrm{cm}$
C.$3\mathrm{cm}$
D.$4\mathrm{cm}$
答案:
C
3. (2024·成都)如图,$\triangle ABC\cong\triangle CDE$,若$\angle D= 35^{\circ}$,$\angle ACB= 45^{\circ}$,则$\angle DCE$的度数为
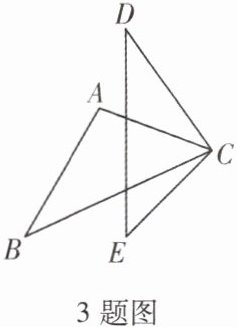
100°
。
答案:
100°
4. 如图,已知$\triangle ABC\cong\triangle DBE$,$\angle A= 36^{\circ}$,$\angle B= 40^{\circ}$,求$\angle AED$的度数。

答案:
∵△ABC≌△DBE,
∴∠D=∠A=36°,∠DBE=∠ABC=40°,∠DEB=∠ACB。
在△ABC中,∠ACB=180°-∠A-∠ABC=180°-36°-40°=104°,
∴∠DEB=∠ACB=104°。
∵点A,E,C在同一直线上(隐含条件,由全等三角形对应顶点位置关系可得),
∴∠AED+∠DEB=180°,
∴∠AED=180°-∠DEB=180°-104°=76°。
76°
∵△ABC≌△DBE,
∴∠D=∠A=36°,∠DBE=∠ABC=40°,∠DEB=∠ACB。
在△ABC中,∠ACB=180°-∠A-∠ABC=180°-36°-40°=104°,
∴∠DEB=∠ACB=104°。
∵点A,E,C在同一直线上(隐含条件,由全等三角形对应顶点位置关系可得),
∴∠AED+∠DEB=180°,
∴∠AED=180°-∠DEB=180°-104°=76°。
76°
5. 如图是$5×5$的正方形网格,$\triangle ABC$的顶点都在小正方形的顶点上,像这样的三角形叫作格点三角形。画与$\triangle ABC$只有一条公共边且全等的格点三角形,在该网格中这样的格点三角形(不与$\triangle ABC$重合)最多可以画出
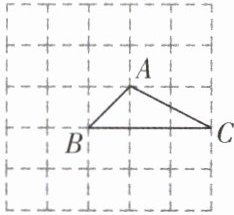
4
个。
答案:
4
三角形全等的判定:两边和它们的夹角
思考
有两边及一角分别对应相等的两个三角形全等吗?
练习
如图,$AB = AC$,$AD = AE$,$\angle 1 = \angle 2$,
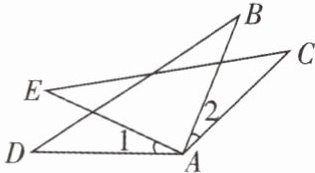
要用边角边基本事实证明$\triangle ABD\cong\triangle ACE$,需要满足的三个条件中,已具备两个条件:
对应相等
的两个三角形全等. (可以简写成“边角边”或“SAS”)思考
有两边及一角分别对应相等的两个三角形全等吗?
不一定
练习
如图,$AB = AC$,$AD = AE$,$\angle 1 = \angle 2$,

要用边角边基本事实证明$\triangle ABD\cong\triangle ACE$,需要满足的三个条件中,已具备两个条件:
AB=AC,AD=AE
,还需要一个条件∠BAD=∠CAE
. 这个条件可以证得吗?可以证得
答案:
对应相等;不一定;AB=AC,AD=AE;∠BAD=∠CAE;可以证得
查看更多完整答案,请扫码查看


