《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

7. 函数 $ y = \frac { \sqrt { x + 3 } } { x } $ 中,自变量 $ x $ 的取值范围是x≥-3且x≠0.

答案： x≥-3且x≠0

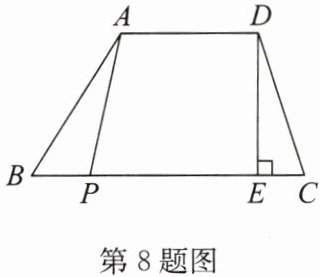
8. 如图,在梯形 $ ABCD $ 中,$ AD // BC $,$ BC = 2AD = 8 $,高 $ DE = 4 $,$ P $ 为边 $ BC $ 上的动点,连接 $ AP $,当 $ BP $ 的长度由小到大变化时,四边形 $ APCD $ 的面积也随之发生变化.
(1)若设 $ BP = x $,四边形 $ APCD $ 的面积为 $ y $,求 $ y $ 与 $ x $ 之间的关系式；
(2)当 $ BP = AD $ 时,求四边形 $ APCD $ 的面积.

答案： 解:
(1)
∵S四边形APCD=S梯形ABCD-S△ABP,
∴y= $\frac{1}{2}$×(4+8)×4- $\frac{1}{2}$×4×x=24-2x.
∴y与x之间的关系式为y=24-2x.
(2)
∵BP=AD,
∴x=4,
∴y=24-2×4=16,
∴四边形APCD的面积为16.

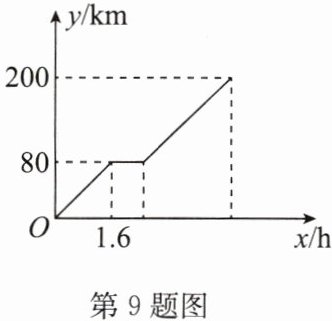
9. 甲、乙两地相距 $ 200 km $,早上 $ 8:00 $ 货车从甲地出发将一批物资运往乙地,途中货车出现了故障,已知货车离甲地的路程 $ y(km) $ 与行驶时间 $ x(h) $ 的关系如图所示.
(1)求货车出现故障前的平均速度；
(2)若货车司机经过 $ 24 min $ 维修排除了故障,继续运送物资去乙地,现要求该批物资运到乙地必须在当天中午 $ 12:00 $ 前,那么货车排除故障后的平均速度应该至少提高到多少?

答案： 解:
(1)80÷1.6=50(km/h). 答:货车出现故障前的平均速度为50 km/h.
(2)设货车排除故障后的平均速度为x km/h, 则(12-1.6- $\frac{24}{60}$-8)x≥200-80,解得x≥60. 答:货车排除故障后的平均速度应该至少提高到60 km/h.

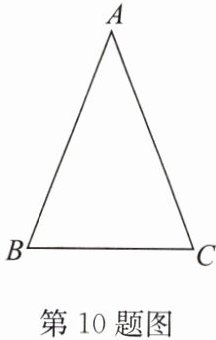
10. 如图,在 $ \triangle ABC $ 中,$ AB = AC = x $,$ BC = y $,该三角形的周长为 $ 20 $.
(1)求 $ y $ 与 $ x $ 之间的函数关系式；
(2)求自变量 $ x $ 的取值范围；
(3)当 $ x $ 的值为多少时,该三角形是等边三角形?

答案： 解:
(1)由题意得2x+y=20,从而y=20-2x.
(2)由题意得$\begin{cases} x+x＞20-2x, \\ x-x＜20-2x, \end{cases}$解得5＜x＜10, 故自变量x的取值范围是5＜x＜10.
(3)由题意得x=20-2x,解得x= $\frac{20}{3}$, 故当x= $\frac{20}{3}$时,该三角形为等边三角形.