《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

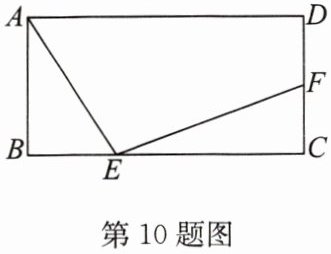
10. 如图,在长方形 $ABCD$ 中,$AB = 6$,$AD = 12$,$E$ 为 $BC$ 边上的动点,$F$ 为 $CD$ 边的中点,连接 $AE$,$EF$,则 $AE + EF$ 的最小值为15。

答案： 15

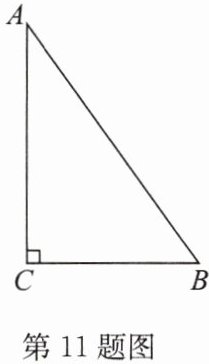
11. (16分)如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AC = 12$,$BC = 9$。
(1)用尺规作 $AB$ 边的垂直平分线 $DE$,交 $AC$ 于点 $E$,交 $AB$ 于点 $D$；(保留作图痕迹,不写作法)
(2)求(1)中 $CE$ 的长。

答案：
解:
(1)如答图,直线DE即为所求.　　　　　　　　
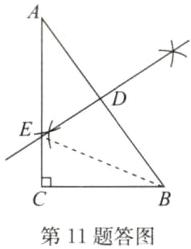
(2)如答图,连接BE.设CE=x,则AE=BE=12-x.在Rt△BEC中,由BC²+CE²=BE²,得x²+9²=(12-x)²,解得x=$\frac{21}{8}$,
∴CE=$\frac{21}{8}$.

12. (16分)如图,有 $A$,$B$,$C$ 三个村庄,它们之间的距离分别是 $AB = 5$ km,$BC = 12$ km,$AC = 13$ km。为助力“乡村振兴”,规划部门计划要从 $B$ 村修一条公路 $BD$,使得 $BD\perp AC$。已知公路的造价为39万元/km,请问修这条公路 $BD$ 的造价是多少万元？

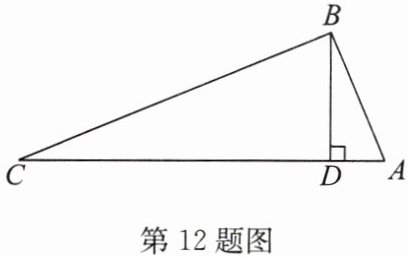
答案： 解:
∵AB=5 km,BC=12 km,AC=13 km,
∴AB²+BC²=AC²,
∴∠ABC=90°.
∵BD⊥AC,
∴S△ABC=$\frac{1}{2}$AB·BC=$\frac{1}{2}$BD·AC,
∴BD=$\frac{AB·BC}{AC}$=$\frac{60}{13}$(km).
∴39×$\frac{60}{13}$=180(万元).答:修这条公路BD的造价是180万元.

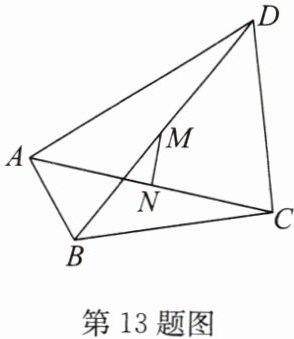
13. (18分)(2024秋·姜堰区期末)如图,在四边形 $ABCD$ 中,$\angle BAD = \angle BCD = 90^{\circ}$。$M$,$N$ 分别是对角线 $BD$,$AC$ 的中点。
(1)求证：$MN\perp AC$；
(2)若 $AC = 6$,$MN = \sqrt{7}$,$BC = 5$,求 $CD$ 的长。

答案：

(1)证明:如答图,连接AM,CM.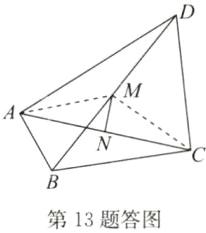　　　　　　　　
∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=CM=$\frac{1}{2}$BD,
∴△AMC是等腰三角形.
∵N是AC的中点,
∴MN⊥AC.
(2)解:
∵N是AC的中点,
∴CN=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3.由
(1)得MN⊥AC,在Rt△CNM中,由勾股定理,得CM=$\sqrt{CN^{2}+MN^{2}}$=$\sqrt{3^{2}+(\sqrt{7})^{2}}$=4.由
(1)得CM=$\frac{1}{2}$BD,
∴BD=2CM=2×4=8.在Rt△BCD中,由勾股定理,得CD=$\sqrt{BD^{2}-BC^{2}}$=$\sqrt{8^{2}-5^{2}}$=$\sqrt{39}$.