第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. (2024·无锡二模)函数 $ y = \frac{2x}{x - 3} $ 中自变量 $ x $ 的取值范围是(
A.$ x > 3 $
B.$ x \geq 3 $
C.$ x \neq 3 $ 且 $ x \neq 0 $
D.$ x \neq 3 $
D
)A.$ x > 3 $
B.$ x \geq 3 $
C.$ x \neq 3 $ 且 $ x \neq 0 $
D.$ x \neq 3 $
答案:
D
2. 下列图象不能体现 $ y $ 是 $ x $ 的函数的是(
]

C
)]

答案:
C
3. (2024·武威)已知函数 $ y = - 2x + 4 $,当自变量 $ x > 2 $ 时,函数 $ y $ 的值可以是
-2(答案不唯一)
(写出一个合理的值即可).
答案:
-2(答案不唯一)
4. 直角三角形的两个锐角分别为 $ x^{\circ} $和 $ y^{\circ} $,则 $ y $ 与 $ x $ 的函数关系式为
y=90-x
,其中自变量 $ x $ 的取值范围是0<x<90
.
答案:
y=90-x 0<x<90
5. 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 如图是小明从家到学校这一过程中离家的距离 $ s $(米)与时间 $ t $(分)之间的关系.
(1)小明从家到学校的路程共
(2)小明修车用了多长时间?
(3)小明修车前和修车后的平均速度分别是多少?
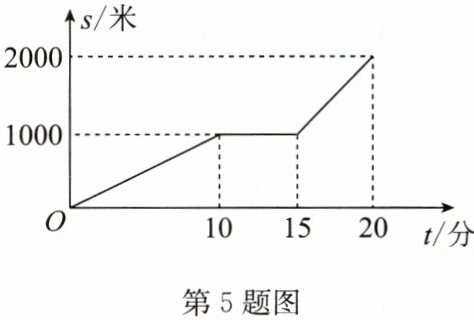
(1)小明从家到学校的路程共
2000
米,从家出发到学校,小明共用了20
分钟;(2)小明修车用了多长时间?
解:小明修车用了15-10=5(分).
(3)小明修车前和修车后的平均速度分别是多少?
解:由题图得,小明修车前的平均速度为1000÷10=100(米/分), 修车后的平均速度为(2000-1000)÷(20-15)=200(米/分).

答案:
(1)2000 20
(2)解:小明修车用了15-10=5(分).
(3)解:由题图得,小明修车前的平均速度为1000÷10=100(米/分), 修车后的平均速度为(2000-1000)÷(20-15)=200(米/分).
(1)2000 20
(2)解:小明修车用了15-10=5(分).
(3)解:由题图得,小明修车前的平均速度为1000÷10=100(米/分), 修车后的平均速度为(2000-1000)÷(20-15)=200(米/分).
6. (2024·江西)将常温中的温度计插入一杯 $ 60^{\circ}C $ 的热水(恒温)中,温度计的读数 $ y(^{\circ}C) $ 与时间 $ x(min) $ 的关系用图象可近似表示为(
]

C
)]

答案:
C
查看更多完整答案,请扫码查看


