《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

5. 在平面直角坐标系中,对于点 $P(x,y)$,我们把点 $P'(y - 1,-x - 1)$ 叫作点 $P$ 的友好点,已知点 $A_1$ 的友好点为点 $A_2$,点 $A_2$ 的友好点为点 $A_3$,点 $A_3$ 的友好点为点 $A_4……$ 以此类推,当点 $A_1$ 的坐标为 $(2,1)$ 时,点 $A_{2023}$ 的坐标为(-4,-1).

答案： (-4,-1)

6. 如图,点 $A_1(1,1)$ 向上平移 $1$ 个单位长度,再向右平移 $2$ 个单位长度,得到点 $A_2$；点 $A_2$ 向上平移 $2$ 个单位长度,再向右平移 $4$ 个单位长度,得到点 $A_3$；点 $A_3$ 向上平移 $4$ 个单位长度,再向右平移 $8$ 个单位长度,得到点 $A_4……$ 按照这个规律平移得到点 $A_n$,则点 $A_n$ 的横坐标为$2^{n}-1$.

答案： $2^{n}-1$

7. 在平面直角坐标系中,对于平面内任一点 $(m,n)$,规定以下两种变换：
① $f(m,n)= (m,m + n)$；② $g(m,n)= (m,m - n)$.
按照以上变换填空：$f(2,1)= $(2,3),$f[f(1,1)]= $(1,3),$f[g(1,1)]= $(1,1).

答案： (2,3) (1,3) (1,1)

8. (2024·绥化)如图,已知 $A_1(1,-\sqrt{3})$,$A_2(3,-\sqrt{3})$,$A_3(4,0)$,$A_4(6,0)$,$A_5(7,\sqrt{3})$,$A_6(9,\sqrt{3})$,$A_7(10,0)$,$A_8(11,-\sqrt{3})$,…$$,以此规律,点 $A_{2024}$ 的坐标为______.

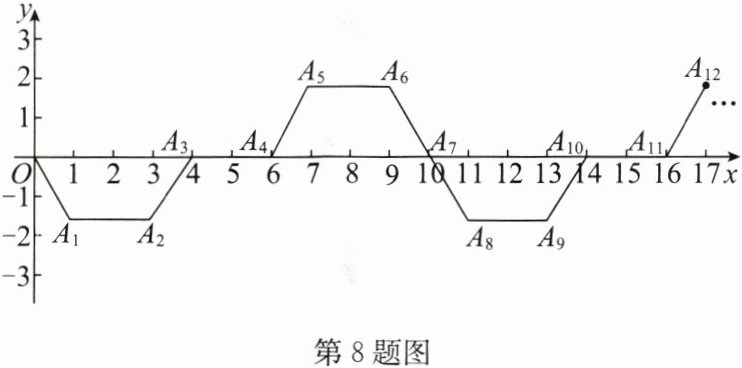
答案： (2891,$-\sqrt{3}$)

9. (2024·枣庄)任取一个正整数,若是奇数,就将该数乘 $3$ 再加上 $1$；若是偶数,就将该数除以 $2$. 反复进行上述两种运算,经过有限次运算后,必进入循环圈 $1\to4\to2\to1$,这就是“冰雹猜想”. 在平面直角坐标系 $xOy$ 中,将点 $(x,y)$ 中的 $x$,$y$ 分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中 $x$,$y$ 均为正整数. 例如,点 $(6,3)$ 经过第 $1$ 次运算得到点 $(3,10)$,经过第 $2$ 次运算得到点 $(10,5)$,以此类推,则点 $(1,4)$ 经过 $2024$ 次运算后得到点的坐标为______(2,1).

答案： (2,1)

10. 如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成的,将护栏的图案放在平面直角坐标系中. 已知小正方形的边长均为 $1$,点 $A_1$ 的坐标为 $(2,2)$,点 $A_2$ 的坐标为 $(5,2)$.
(1) 点 $A_3$ 的坐标为(8,2),点 $A_n$ 的坐标为(3n-1,2)(用含 $n$ 的代数式表示)；
(2) 若护栏长为 $2020$,则需要674个小正方形,673个大正方形.

答案：
(1)(8,2) (3n-1,2)
(2)674 673