《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

2.【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图①是著名的“赵爽弦图”,由四个全等的直角三角形拼成,用它可以证明勾股定理.思路是大正方形的面积有两种求法,一种是等于$ c^{2} $,另一种是等于四个直角三角形与一个小正方形的面积之和,即$ \frac{1}{2}ab×4+(b - a)^{2} $,从而得到等式$ c^{2}= \frac{1}{2}ab×4+(b - a)^{2} $,化简便得结论$ a^{2}+b^{2}= c^{2} $.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.

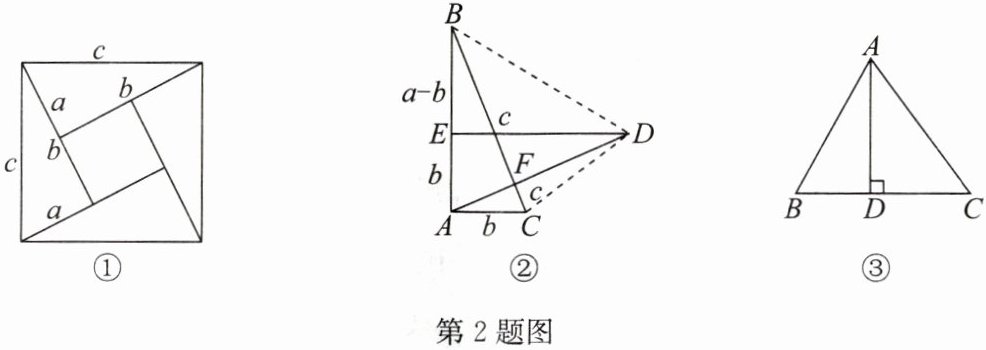
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新证法：把两个全等的直角$ \triangle ABC 和 \triangle DEA $如图②方式放置,其三边长分别为$ a,b,c,\angle BAC= \angle DEA = 90^{\circ} $,显然$ BC\perp AD $.
(1)请用$ a,b,c 分别表示出四边形 ABDC $,梯形$ AEDC $,$ \triangle BED $的面积,再探究这三个图形面积之间的关系,证明勾股定理$ a^{2}+b^{2}= c^{2} $；
【方法迁移】(2)如图③,在$ \triangle ABC $中,$ AD 是 BC $边上的高,$ AB = 4,AC = 5,BC = 6 $,设$ BD = x $,求$ x $的值.

答案： 2. 解:
(1)由题意得$S_{四边形ABDC}=\frac {1}{2}c^{2},$
$S_{梯形AEDC}=\frac {1}{2}(b+a)b,S_{\triangle BED}=\frac {1}{2}(a-b)a.$
$\because S_{四边形ABDC}=S_{梯形AEDC}+S_{\triangle BED},$
$\therefore \frac {1}{2}c^{2}=\frac {1}{2}(b+a)b+\frac {1}{2}(a-b)a,$
$\therefore \frac {1}{2}c^{2}=\frac {1}{2}b^{2}+\frac {1}{2}ab+\frac {1}{2}a^{2}-\frac {1}{2}ab,$
$\therefore a^{2}+b^{2}=c^{2}.$
(2)在$Rt\triangle ABD$中,由勾股定理,得$AD^{2}=AB^{2}-BD^{2}=4^{2}-x^{2}=16-x^{2}.$
$\because BD+CD=BC=6,$
$\therefore CD=BC-BD=6-x.$
在$Rt\triangle ACD$中,由勾股定理,得$AD^{2}=AC^{2}-CD^{2}=5^{2}-(6-x)^{2}=-11+12x-x^{2},$
$\therefore 16-x^{2}=-11+12x-x^{2},\therefore x=\frac {9}{4}.$