《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

11. 古希腊哲学家柏拉图曾指出,如果$m表示大于1$的整数,$a = 2m$,$b = m^{2}-1$,$c = m^{2}+1$,那么长分别为$a$,$b$,$c$的三条线段首尾顺次相接,形成的三角形是什么形状？请说明理由.

答案： 解:直角三角形.理由如下:
∵m表示大于1的整数,a=2m,b=m²−1,c=m²+1,
∴c−a=m²+1−2m=(m−1)²＞0,
∴c＞a.
∵a²+b²=(2m)²+(m²−1)²=4m²+m⁴−2m²+1=(m²+1)²,c²=(m²+1)²,
∴a²+b²=c²,
∴长分别为a,b,c的三条线段首尾顺次相接,形成的是直角三角形

12. (2024·宿迁共同体期末)如图是一块地,已知$AD = 8\mathrm{cm}$,$CD = 6\mathrm{cm}$,$\angle D = 90^{\circ}$,$AB = 26\mathrm{cm}$,$BC = 24\mathrm{cm}$,求这块地的面积.

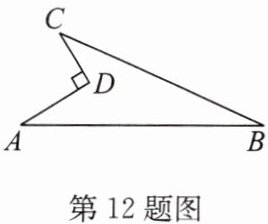
答案： 解:如答图,连接AC.
∵AD=8cm,CD=6cm,∠D=90°,
∴AC= $\sqrt{6^{2}+8^{2}}$=10(cm).
∵AB=26cm,BC=24cm,10²+24²=26²,即AC²+BC²=AB²,
∴△ABC为直角三角形,∠ACB=90°.
∴S四边形ABCD=S△ABC−S△ACD=$\frac{1}{2}$×10×24−$\frac{1}{2}$×6×8=96(cm²).

13. (2024·宿豫期中)如图,在$\triangle ABC$中,$AD\perp BC$,垂足为$D$,且$AB = 15$,$AD = 12$,$CD = 16$.求证：$\triangle ABC$是直角三角形.

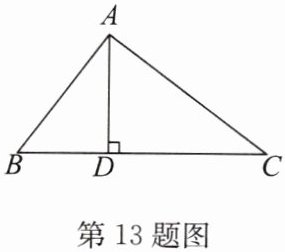
答案： 证明:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,又
∵AB=15,AD=12,CD=16,
∴BD²=AB²−AD²=15²−12²=225−144=81,AC²=CD²+AD²=16²+12²=256+144=400.
∴BD=9,AC=20.
∴BC=BD+CD=9+16=25.
∵AB²+AC²=15²+20²=225+400=625,BC²=25²=625,
∴BC²=AB²+AC²,
∴△ABC是直角三角形