《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

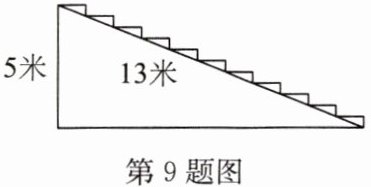
9. 某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯.已知楼梯的总高度为5米,楼梯长13米,主楼道宽2米.这种红色地毯的售价为每平方米30元,其侧面如图所示,则购买这种红色地毯至少需要1020元.

答案： 1020

10. 如图,在笔直的河流一侧有一旅游地$C$,河边有两个景点$A$,$B$,其中$AB = AC$,因$C到A$的路不通,为方便游客,决定在河边修建一个景点$H$($A$,$H$,$B$三点在同一直线上),并修建一条路$CH$,测得$BC = 10$千米,$CH = 8$千米,$BH = 6$千米.
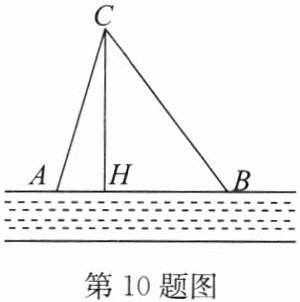
(1)判断$\triangle BCH$的形状,并说明理由；
(2)求原路线$AC$的长.

答案：
(1)△BCH是直角三角形,理由:
∵BC=10千米,CH=8千米,BH=6千米,
∴CH²+BH²=BC²,
∴∠CHB=90°,
∴△BCH是直角三角形.
(2)设AC=x千米,则AH=(x-6)千米.在Rt△ACH中,由勾股定理,得AH²+CH²=AC²,
∴(x-6)²+8²=x²,解得x=25/3.
∴原路线AC的长为25/3千米.

11. 如图,秋千$OA$静止的时候,踏板离地高一尺($AC = 1$尺),将它往前推进十尺($EB = 10$尺),此时踏板升高,离地五尺($BD = 5$尺).求秋千绳索$OB$的长度.

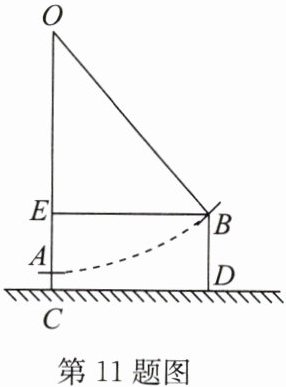
答案： 解:设秋千绳索OB的长度为x尺,则OA=OB=x尺.
∵AE=EC-AC=4(尺),
∴OE=(x-4)尺.在Rt△OBE中,由勾股定理,得(x-4)²+10²=x²,解得x=14.5.故秋千绳索OB的长度为14.5尺.