第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
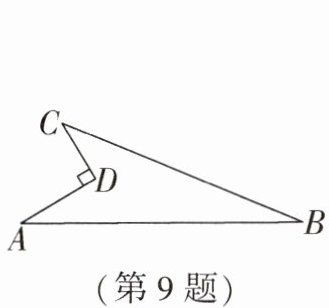
9. 如图,在凹四边形ABCD中,∠ADC= 90°,AD= 4,CD= 3,AB= 13,BC= 12,则四边形ABCD的面积为______.

答案:
24
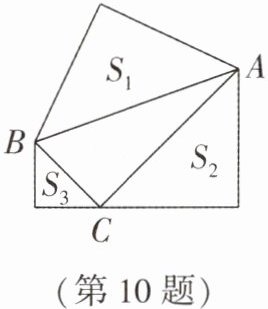
10. 如图,以△ABC的三边为斜边,向外作等腰直角三角形,其面积分别是$S_1,S_2,S_3$,且$S_1= 25,S_2= 16$,当$S_3= $______时,∠ACB= 90°.

答案:
9
11. 张老师在一次“探究性学习”课中,设计了如下数表:
| n | 2 | 3 | 4 | 5 | ... |
| a | $2^2-1$ | $3^2-1$ | $4^2-1$ | $5^2-1$ | ... |
| b | 4 | 6 | 8 | 10 | ... |
| c | $2^2+1$ | $3^2+1$ | $4^2+1$ | $5^2+1$ | ... |
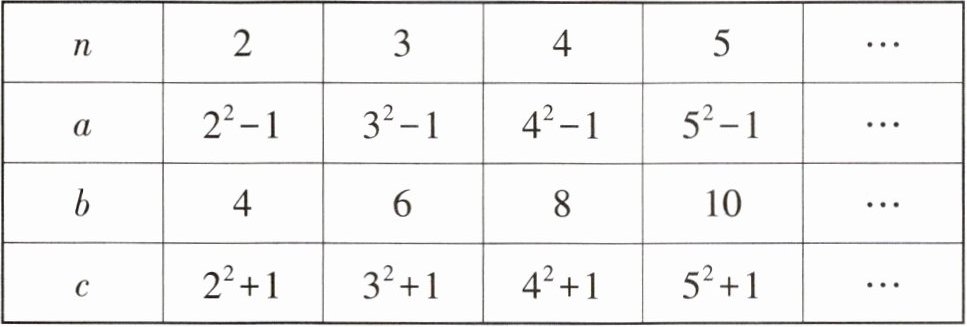
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= ______,b= ______,c= ______;
(2)猜想:以a,b,c为边的三角形是否为直角三角形,并证明你的猜想.
| n | 2 | 3 | 4 | 5 | ... |
| a | $2^2-1$ | $3^2-1$ | $4^2-1$ | $5^2-1$ | ... |
| b | 4 | 6 | 8 | 10 | ... |
| c | $2^2+1$ | $3^2+1$ | $4^2+1$ | $5^2+1$ | ... |

(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= ______,b= ______,c= ______;
(2)猜想:以a,b,c为边的三角形是否为直角三角形,并证明你的猜想.
答案:
(1)$n^{2}-1$ $2n$ $n^{2}+1$
(2)以 a,b,c 为边的三角形是直角三角形.证明如下:
∵ $a=n^{2}-1$,$b=2n$,$c=n^{2}+1$,
∴ $a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}-2n^{2}+1+4n^{2}=n^{4}+2n^{2}+1=(n^{2}+1)^{2}$,而 $c^{2}=(n^{2}+1)^{2}$,
∴ $a^{2}+b^{2}=c^{2}$,即以 a,b,c 为边的三角形是直角三角形.
(2)以 a,b,c 为边的三角形是直角三角形.证明如下:
∵ $a=n^{2}-1$,$b=2n$,$c=n^{2}+1$,
∴ $a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}-2n^{2}+1+4n^{2}=n^{4}+2n^{2}+1=(n^{2}+1)^{2}$,而 $c^{2}=(n^{2}+1)^{2}$,
∴ $a^{2}+b^{2}=c^{2}$,即以 a,b,c 为边的三角形是直角三角形.
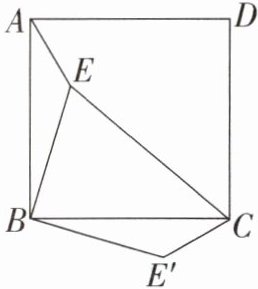
12. (几何直观·推理能力)如图,点E是正方形ABCD内的一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置.若AE= 1,BE= 2,CE= 3,求∠AEB的度数.

答案:
连接 $EE'$.
∵ △ABE 绕点 B 顺时针旋转 $90^{\circ}$到△$CBE'$的位置,
∴ $\angle EBE'=90^{\circ}$,
∴ △$EBE'$是直角三角形.
∵ △ABE 与△$CBE'$全等,
∴ $AE=CE'=1$,$BE=BE'=2$,$\angle AEB=\angle CE'B$,
∴ $\angle BEE'=\angle BE'E=45^{\circ}$,
∴ $EE'^{2}=2^{2}+2^{2}=8$.又
∵ $EC=3$,
∴ $EC^{2}=E'C^{2}+EE'^{2}$,
∴ △$EE'C$是直角三角形,
∴ $\angle EE'C=90^{\circ}$,
∴ $\angle BE'C=\angle BE'E+\angle EE'C=135^{\circ}$,
∴ $\angle AEB=135^{\circ}$.
∵ △ABE 绕点 B 顺时针旋转 $90^{\circ}$到△$CBE'$的位置,
∴ $\angle EBE'=90^{\circ}$,
∴ △$EBE'$是直角三角形.
∵ △ABE 与△$CBE'$全等,
∴ $AE=CE'=1$,$BE=BE'=2$,$\angle AEB=\angle CE'B$,
∴ $\angle BEE'=\angle BE'E=45^{\circ}$,
∴ $EE'^{2}=2^{2}+2^{2}=8$.又
∵ $EC=3$,
∴ $EC^{2}=E'C^{2}+EE'^{2}$,
∴ △$EE'C$是直角三角形,
∴ $\angle EE'C=90^{\circ}$,
∴ $\angle BE'C=\angle BE'E+\angle EE'C=135^{\circ}$,
∴ $\angle AEB=135^{\circ}$.
查看更多完整答案,请扫码查看


