《2025年名校课堂九年级数学上册北师大版山西专版》

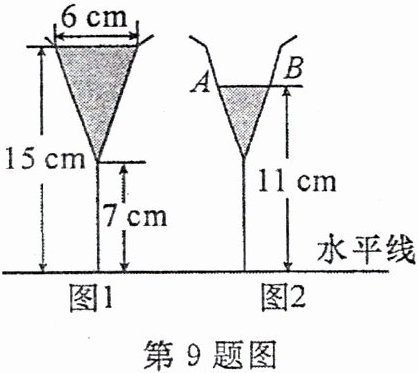
9. 新考向 真实情境 图1所示的是装了液体的高脚杯示意图(数据如图)，用去一部分液体后如图2所示，此时液面$AB=$(C)

A.$1cm$
B.$2cm$
C.$3cm$
D.$4cm$

答案： 9.C

10. 如图，在$\triangle ABC$中，点$D$，$E$分别在$AB$，$AC$上，$AF$平分$\angle BAC$交$DE$于点$G$。若$AE = 3$，$EC = 1$，$AD = 2$，$BD = 4$，则$AG:AF$的值为\frac{1}{2}。

答案： $10.\frac{1}{2}$

11. 如图，已知$\triangle ABC\sim\triangle A'B'C'$，它们的相似比为$k$，$AD$，$A'D'$是对应的中线。求证：$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k$。
]

答案： 11.证明：
∵△ABC∽△A'B'C'，
∴$\frac{AB}{A'B'}=\frac{BC}{B'C'}=k,∠B=∠B'.$
∵AD,A'D'分别是△ABC,△A'B'C'的中线，
∴$BD=\frac{1}{2}BC,B'D'=\frac{1}{2}B'C'.$
∵$\frac{BD}{B'D'}=\frac{\frac{1}{2}BC}{\frac{1}{2}B'C'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}=k.$
∴△ABD∽△A'B'D'.
∴$\frac{AD}{A'D'}=\frac{AB}{A'B'}=k.$

12. 如图所示的是一个照相机成像的示意图，像高$MN$，景物高度$AB$，$CD$为水平视线，根据物体成像原理知：$AB// MN$，$CD\perp MN$。
(1) 如果像高$MN$是$35mm$，焦距$CL$是$50mm$，拍摄的景物高度$AB$是$4.9m$，那么拍摄点离景物的距离$LD$是多少？
(2) 如果要完整地拍摄高度是$2m$的景物，拍摄点离景物有$4m$，像高不变，那么相机的焦距应调整为70$mm$。
]

答案： 12.解：
(1)
∵AB//MN,
∴∠M=∠B,∠N=∠A.
∴△LMN∽△LBA.
∴$\frac{MN}{BA}=\frac{LC}{LD},$即$\frac{MN}{LC}=\frac{BA}{LD}.\frac{35}{50}=\frac{4.9}{LD}.$
∴LD=7m.答：拍摄点离景物的距离LD是7m.
(2)70

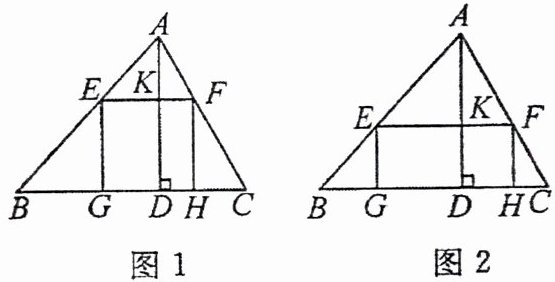
13. (1) 如图1，一块材料的形状是锐角三角形($\triangle ABC$)，边$BC = 120mm$，高$AD = 80mm$。把它加工成正方形零件，使正方形的一边在$BC$上，其余两个顶点分别在$AB$，$AC$上，则这个正方形零件的边长是48$mm$。
(2) 若(1)中要加工的零件是一个矩形，且此矩形两条边$EF:EG = 5:2$，如图2所示，求

此

时$EF$的长。
]

答案： 13.解：
(1)48
(2)
∵EF：EG=5：2，
∴设EF=5xmm,EG=2xmm.
∵四边形GEFH是矩形，AD⊥BC，
∴四边形GEKD是矩形.
∴EG=KD=2xmm,AK=(80-2x)mm.
∵EF//BC，
∴△AEF∽△ABC.
∵AD⊥BC，
∴$\frac{EF}{BC}=\frac{AK}{AD},$即$\frac{5x}{120}=\frac{80-2x}{80}.$解得x=15.
∴EF=5x=75mm.答：EF的长为75mm.