第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
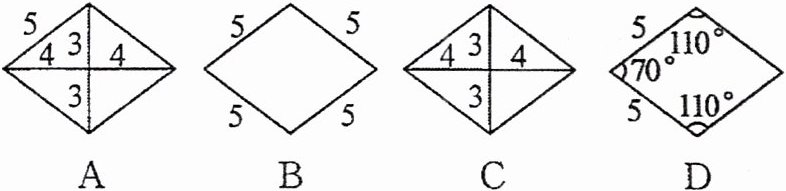
9. (2024·太原期中)依据所标数据,下列四边形不一定为菱形的是( )

答案:
9.C
10. 如图,在四边形$ABCD$中,$E$,$F$,$G$,$H$分别是$AB$,$CD$,$AC$,$BD$的中点,添加下列条件,可以判定四边形$EHFG$为菱形的是(
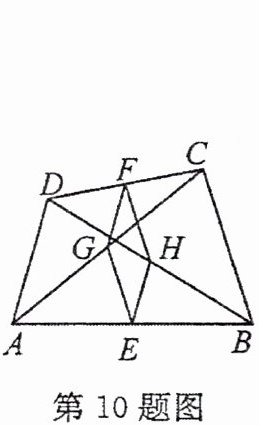
A.$AC = BD$
B.$AB// CD$
C.$AD = BC$
D.$AC\perp BD$
C
)
A.$AC = BD$
B.$AB// CD$
C.$AD = BC$
D.$AC\perp BD$
答案:
10.C
11. 如图,线段$AB$,$CD$端点的坐标分别为$A(-1,2)$,$B(3,-1)$,$C(3,2)$,$D(-1,5)$,且$AB// CD$,将$CD$平移至第一象限内,得到$C'D'$($C'$,$D'$均在格点上). 要使四边形$ABC'D'$是菱形,则所有满足条件的点$D'$的坐标为

(3,5)或(2,6)
.
答案:
11.(3,5)或(2,6)
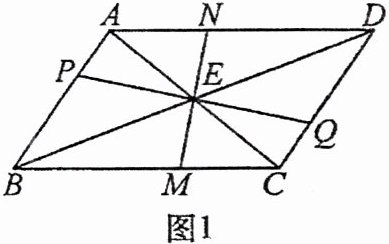
12. 如图 1,$□ ABCD$的对角线$AC$,$BD$相交于点$E$,过点$E$作两条互相垂直的线段,分别交边$AB$,$BC$,$CD$,$DA$于点$P$,$M$,$Q$,$N$.
(1) 求证:$\triangle PBE\cong\triangle QDE$.
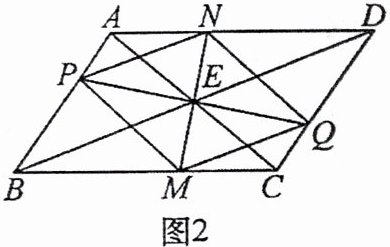
(2) 如图 2,顺次连接点$P$,$M$,$Q$,$N$,求证:四边形$PMQN$是菱形.
(1) 求证:$\triangle PBE\cong\triangle QDE$.
(2) 如图 2,顺次连接点$P$,$M$,$Q$,$N$,求证:四边形$PMQN$是菱形.


答案:
12.证明:
(1)
∵四边形ABCD是平行四边形,
∴EB = ED,AB//CD.
∴∠EBP = ∠EDQ.在△PBE和△QDE中,$\begin{cases} \angle EBP = \angle EDQ \\ EB = ED \\ \angle BEP = \angle DEQ \end{cases}$
∴△PBE≌△QDE(ASA).
(2)
∵△PBE≌△QDE,
∴EP = EQ.同理可证,△BME≌△DNE.
∴EM = EN.四边形PMQN是平行四边形.
∵PQ⊥MN,
∴平行四边形PMQN是菱形.
(1)
∵四边形ABCD是平行四边形,
∴EB = ED,AB//CD.
∴∠EBP = ∠EDQ.在△PBE和△QDE中,$\begin{cases} \angle EBP = \angle EDQ \\ EB = ED \\ \angle BEP = \angle DEQ \end{cases}$
∴△PBE≌△QDE(ASA).
(2)
∵△PBE≌△QDE,
∴EP = EQ.同理可证,△BME≌△DNE.
∴EM = EN.四边形PMQN是平行四边形.
∵PQ⊥MN,
∴平行四边形PMQN是菱形.
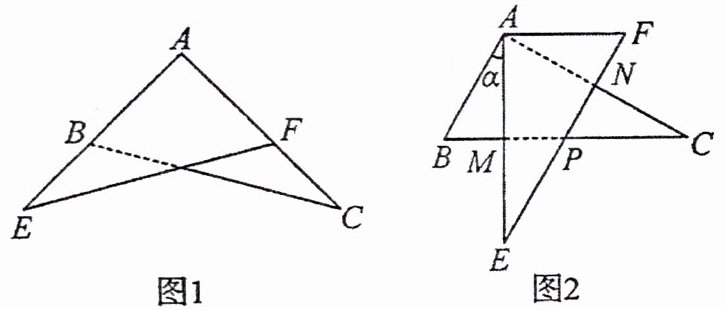
13. 某校九年级学习小组在探究学习过程中,用两块完全相同的且含$60^{\circ}$角的直角三角板$ABC$与$AFE$按如图 1 所示的位置放置,现将$\mathrm{Rt}\triangle AEF$绕点$A$按逆时针方向旋转角$\alpha(0^{\circ}<\alpha<90^{\circ})$,如图 2,$AE$与$BC$交于点$M$,$AC$与$EF$交于点$N$,$BC$与$EF$交于点$P$.
(1) 求证:$BM = FN$.
(2) 当旋转角$\alpha = 30^{\circ}$时,四边形$ABPF$是什么样的特殊四边形?并说明理由.
(1) 求证:$BM = FN$.
(2) 当旋转角$\alpha = 30^{\circ}$时,四边形$ABPF$是什么样的特殊四边形?并说明理由.

答案:
13.解:
(1)证明:由题意,得AB = AF,∠BAM = ∠FAN.在△ABM和△AFN中,$\begin{cases} \angle BAM = \angle FAN \\ AB = AF \\ \angle B = \angle F \end{cases}$
∴△ABM≌△AFN(ASA).
∴BM = FN.
(2)当旋转角α = 30°时,四边形ABPF是菱形.理由:
∵α = 30°,∠EAF = 90°,
∴∠FAB = 120°.
∵∠B = 60°,
∴∠B + ∠FAB = 180°.
∴AF//BP.
∴∠FPC = ∠F = 60°.
∴∠FPC = ∠B = 60°.
∴AB//FP.
∴四边形ABPF是平行四边形.又
∵AB = AF,
∴平行四边形ABPF是菱形.
(1)证明:由题意,得AB = AF,∠BAM = ∠FAN.在△ABM和△AFN中,$\begin{cases} \angle BAM = \angle FAN \\ AB = AF \\ \angle B = \angle F \end{cases}$
∴△ABM≌△AFN(ASA).
∴BM = FN.
(2)当旋转角α = 30°时,四边形ABPF是菱形.理由:
∵α = 30°,∠EAF = 90°,
∴∠FAB = 120°.
∵∠B = 60°,
∴∠B + ∠FAB = 180°.
∴AF//BP.
∴∠FPC = ∠F = 60°.
∴∠FPC = ∠B = 60°.
∴AB//FP.
∴四边形ABPF是平行四边形.又
∵AB = AF,
∴平行四边形ABPF是菱形.
查看更多完整答案,请扫码查看


