《2025年名校课堂九年级数学上册北师大版山西专版》

1. (2023·太原三十六中月考)下列方程一定是一元二次方程的是(D)

A.$ x+\frac{1}{x}=1 $
B.$ x^{2}+3=(x - 1)^{2} $
C.$ ax^{2}+bx+c=0 $
D.$ x^{2}-1=0 $

答案： 1.D

2. (2024·太原期中)将一元二次方程$ (x + 1)(x - 1)=x $化成一般形式正确的是(B)

A.$ x^{2}-x + 1=0 $
B.$ x^{2}-x - 1=0 $
C.$ x^{2}+x + 1=0 $
D.$ x^{2}+x - 1=0 $

答案： 2.B

3. (2024·南充)已知$ m $是方程$ x^{2}+4x - 1=0 $的一个根,则$ (m + 5)(m - 1) $的值为-4.

答案： 3.-4

4. (2024·晋中介休市模拟)用配方法解一元二次方程$ x^{2}-8x + 7=0 $,方程可变形为(B)

A.$ (x + 4)^{2}=9 $
B.$ (x - 4)^{2}=9 $
C.$ (x - 8)^{2}=16 $
D.$ (x + 8)^{2}=57 $

答案： 4.B

5. 已知直角三角形的两条直角边长恰好是方程$ x^{2}-5x + 6=0 $的两个根,则此直角三角形的斜边长是(A)

A.$ \sqrt{13} $
B.$ \sqrt{5} $
C.13
D.5

答案： 5.A

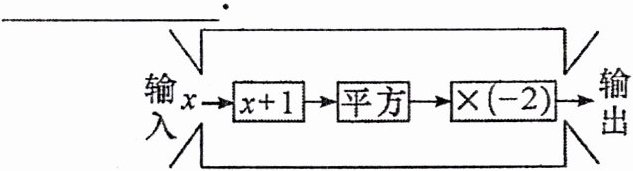
6. 如图所示的是一个简单的计算程序,如果输出的数值为$-10$,那么输入$ x $的值为\sqrt{5}-1 或 -\sqrt{5}-1.

答案： $6.\sqrt{5}-1 $或$ -\sqrt{5}-1$

7. 解方程:
(1)$ 2x^{2}-4x - 5=0 $.
(2)$ 5x(3x + 2)=6x + 4 $.

答案： 7.解：
(1)
∵a=2,b=-4,c=-5.
∴$△=(-4)^2-4×2×(-5)=56＞0. $
∴$x=\frac{4 \pm 2\sqrt{14}}{2 × 2}=\frac{2 \pm \sqrt{14}}{2} $
∴$x_1=\frac{2+\sqrt{14}}{2},x_2=\frac{2-\sqrt{14}}{2}.(2)5x(3x+2)=2(3x+2)(3x+2)(5x-2)=0. $
∴3x+2=0 或 5x-2=0.
∴$x_1=-\frac{2}{3},x_2=\frac{2}{5}.$

8. 若在方程$ □ x^{2}-x + 2=0 $的$ □ $中添加一个合适的数字,使该方程没有实数根,则添加的数字可以是(B)

A.0
B.1
C.$ \frac{1}{10} $
D.$-2$

答案： 8.B

9. (2024·长治长子县期中)小华和小麦对关于$ x $的一元二次方程$ ax^{2}+bx + c=0(a\neq0) $展开讨论,小华说:“若$ c = 0 $,则此方程一定有实数根.”小麦说:“若$ a,c $异号,则此方程一定有实数根.”下列判断正确的是(C)

A.小华正确,小麦错误
B.小华错误,小麦正确
C.小华、小麦都正确
D.小华、小麦都错误

答案： 9.C

10. 如图,矩形$ ABCD $的周长为 12,面积为 5,且$ AB $和$ BC $的长恰好是方程$ x^{2}+mx + n=0 $的两根,则$ m = $-6, $ n = $5.

答案： 10.-6 5

11. (2024·晋中寿阳县多校期中)已知关于$ x $的一元二次方程$ x^{2}+2(m + 2)x + m^{2}-5=0 $.
(1)当方程有两个实数根时,求$ m $的取值范围.
(2)当方程的两个根$ x_{1},x_{2} $满足$ x_{1}^{2}+x_{2}^{2}=x_{1}x_{2}+16 $时,求$ m $的值.

答案： 11.解：
(1)
∵关于x的一元二次方程$x^2+2(m+2)x+m^2-5=0$有两个实数根，
∴$△=[2(m+2)]^2-4×1×(m^2-5)=16m+36≥0，$解得$m≥-\frac{9}{4}.(2)$
∵关于x的一元二次方程$x^2+2(m+2)x+m^2-5=0$的两个根分别为$x_1,x_2,$
∴$x_1+x_2=-2(m+2),x_1x_2=m^2-5. $
∵$x_1^2+x_2^2=x_1x_2+16.$
∴$(x_1+x_2)^2-3x_1x_2=16，$即$[-2(m+2)]^2-3(m^2-5)=16.$整理，得$m^2+16m+15=0，$
∴(m+15)(m+1)=0，解得$m_1=-15,m_2=-1.$
∵$m≥-\frac{9}{4}，$
∴m的值为-1.

12. (2024·晋中祁县模拟改编)上党腊驴肉是山西长治的传统名吃,其肉质肥而不腻、瘦而不柴,香味四溢、回味无穷.某特产专卖店购进一批袋装上党腊驴肉,进价为 40 元/袋,经市场调查发现,当销售单价为 60 元时,每天可售出 300 袋;销售单价每降低 0.5 元,每天可多售出 10 袋.若销售单价降低$ x $元,该专卖店每天销售这种腊驴肉可获得利润 5000 元,则可列方程为(D)


A.$ (60 - 40 + x)(300 + 20x)=5000 $
B.$ (60 - 40 + x)(300 - 20x)=5000 $
C.$ (60 - 40 - x)(300 - 20x)=5000 $
D.$ (60 - 40 - x)(300 + 20x)=5000 $

答案： 12.D