第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (2024·山西省实验中学月考)下列性质中,菱形一定具有的是 (
A.对角线相等
B.有一个角是直角
C.对角线互相垂直
D.四个角相等
C
)A.对角线相等
B.有一个角是直角
C.对角线互相垂直
D.四个角相等
答案:
1.C
2. (2024·太原部分学校段考)如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形 $ABCD$. 若 $\angle ABC = 50^{\circ}$, 则 $\angle DAC$ 的度数为 (
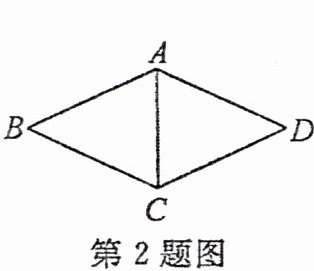
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
答案:
2.C
3. 新考向 开放性问题 如图, $□ ABCD$ 的对角线 $AC$, $BD$ 相交于点 $O$, 点 $E$, $F$, $G$, $H$ 分别是 $OA$, $OB$, $OC$, $OD$ 的中点. 若要使四边形 $EFGH$ 成为菱形, 则 $□ ABCD$ 应满足的条件是

$AB=AD$(答案不唯一)
(写出一种即可).
答案:
3.$AB=AD$(答案不唯一)
4. (2024·侯马市期末)中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴. 如图所示的中国结可近似地看为一个菱形, 菱形 $ABCD$ 的周长为 $80\mathrm{cm}$, 对角线 $BD$ 的长为 $24\mathrm{cm}$, 则对角线 $AC$ 的长为

$32 cm$
.
答案:
4.$32 cm$
5. 新考向 真实情境 如图, 四边形 $ABCD$ 是一个风筝的框架示意图, $G$ 为 $AC$ 的中点, 四边形 $AECF$ 是菱形, $\angle ABC = \angle ADC = 90^{\circ}$.
(1) 若 $\angle EAF = 60^{\circ}$, 求证: 四边形 $ABGD$ 是菱形.
(2) 若 $AB = 2$, $BC = 4$, 求菱形 $AECF$ 的面积.
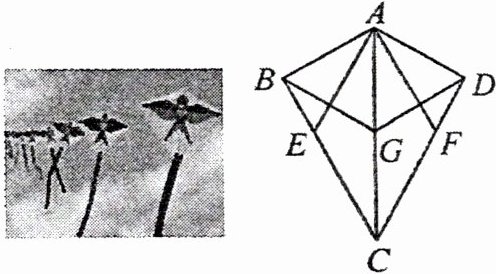
(1) 若 $\angle EAF = 60^{\circ}$, 求证: 四边形 $ABGD$ 是菱形.
(2) 若 $AB = 2$, $BC = 4$, 求菱形 $AECF$ 的面积.

答案:
5.解:
(1)证明:$\because$四边形$AECF$是菱形,$\therefore \angle ECF = \angle EAF = 60°$,$\angle ACE = \angle ACF = \frac{1}{2} \angle ECF = \frac{1}{2} × 60° = 30°$。$\because \angle ABC = \angle ADC = 90°$,$\therefore AB = AD = \frac{1}{2}AC$。$\because G$为$AC$的中点,$\therefore BG = DG = \frac{1}{2}AC$,$\therefore AB = AD = BG = DG$,$\therefore$四边形$ABGD$是菱形。
(2)连接$EF$。$\because$四边形$AECF$是菱形,$\therefore EF \perp AC$,且$EF$经过$AC$的中点$G$,$EF = 2EG$,$AE = CE$,$\therefore \angle AGE = 90°$。在$Rt \triangle ABC$中,由勾股定理,得$AC = \sqrt{AB^2 + BC^2} = \sqrt{2^2 + 4^2} = 2\sqrt{5}$,$\therefore AG = \frac{1}{2}AC = \frac{1}{2} × 2\sqrt{5} = \sqrt{5}$。在$Rt \triangle ABE$中,由勾股定理,得$AE^2 = AB^2 + BE^2$,即$AE^2 = 2^2 + (4 - AE)^2$,解得$AE = \frac{5}{2}$。在$Rt \triangle AGE$中,由勾股定理,得$EG = \sqrt{AE^2 - AG^2} = \sqrt{\left(\frac{5}{2}\right)^2 - (\sqrt{5})^2} = \frac{\sqrt{5}}{2}$,$\therefore EF = 2EG = 2 × \frac{\sqrt{5}}{2} = \sqrt{5}$,$\therefore S_{菱形 AECF} = \frac{1}{2}AC \cdot EF = \frac{1}{2} × 2\sqrt{5} × \sqrt{5} = 5$。
(1)证明:$\because$四边形$AECF$是菱形,$\therefore \angle ECF = \angle EAF = 60°$,$\angle ACE = \angle ACF = \frac{1}{2} \angle ECF = \frac{1}{2} × 60° = 30°$。$\because \angle ABC = \angle ADC = 90°$,$\therefore AB = AD = \frac{1}{2}AC$。$\because G$为$AC$的中点,$\therefore BG = DG = \frac{1}{2}AC$,$\therefore AB = AD = BG = DG$,$\therefore$四边形$ABGD$是菱形。
(2)连接$EF$。$\because$四边形$AECF$是菱形,$\therefore EF \perp AC$,且$EF$经过$AC$的中点$G$,$EF = 2EG$,$AE = CE$,$\therefore \angle AGE = 90°$。在$Rt \triangle ABC$中,由勾股定理,得$AC = \sqrt{AB^2 + BC^2} = \sqrt{2^2 + 4^2} = 2\sqrt{5}$,$\therefore AG = \frac{1}{2}AC = \frac{1}{2} × 2\sqrt{5} = \sqrt{5}$。在$Rt \triangle ABE$中,由勾股定理,得$AE^2 = AB^2 + BE^2$,即$AE^2 = 2^2 + (4 - AE)^2$,解得$AE = \frac{5}{2}$。在$Rt \triangle AGE$中,由勾股定理,得$EG = \sqrt{AE^2 - AG^2} = \sqrt{\left(\frac{5}{2}\right)^2 - (\sqrt{5})^2} = \frac{\sqrt{5}}{2}$,$\therefore EF = 2EG = 2 × \frac{\sqrt{5}}{2} = \sqrt{5}$,$\therefore S_{菱形 AECF} = \frac{1}{2}AC \cdot EF = \frac{1}{2} × 2\sqrt{5} × \sqrt{5} = 5$。
6. (2023·怀仁市期中)如图, 在 $\triangle ABC$ 中, $DE // CA$, $DF // BA$, 下列四个判断不正确的是 (

A.四边形 $AEDF$ 是平行四边形
B.如果 $\angle BAC = 90^{\circ}$, 那么四边形 $AEDF$ 是矩形
C.如果 $AD$ 平分 $\angle BAC$, 那么四边形 $AEDF$ 是矩形
D.如果 $AD \perp BC$, 且 $AB = AC$, 那么四边形 $AEDF$ 是菱形
C
)
A.四边形 $AEDF$ 是平行四边形
B.如果 $\angle BAC = 90^{\circ}$, 那么四边形 $AEDF$ 是矩形
C.如果 $AD$ 平分 $\angle BAC$, 那么四边形 $AEDF$ 是矩形
D.如果 $AD \perp BC$, 且 $AB = AC$, 那么四边形 $AEDF$ 是菱形
答案:
6.C
7. (2024·阳泉盂县二模)如图, 在矩形 $ABCD$ 中, 对角线 $AC$, $BD$ 相交于点 $O$, $AC = 2AB$, 在 $BC$ 上截取 $BE = AB$, 连接 $AE$, $OE$, 则 $\angle AEO$ 的度数为
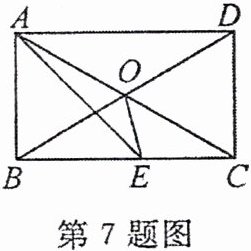
$30°$
.
答案:
7.$30°$
8. (教材 $P27$ 复习题 $T14$ 变式)如图, 在 $□ ABCD$ 中, $\angle B = 60^{\circ}$, $AB = 4$, $AD = 6$, 动点 $F$ 从点 $D$ 出发, 以 $1$ 个单位长度每秒的速度从点 $D$ 向点 $A$ 运动, 同时动点 $E$ 以相同速度从点 $C$ 出发, 沿 $BC$ 方向在 $BC$ 的延长线上运动. 设运动时间为 $t\mathrm{s}$, 连接 $DE$, $CF$. 探究: ①当 $t =$
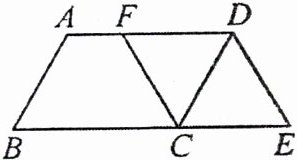
4
, 四边形 $DECF$ 是菱形; ②当 $t =$ 2
, 四边形 $DECF$ 是矩形.
答案:
8.4 2
查看更多完整答案,请扫码查看


