第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
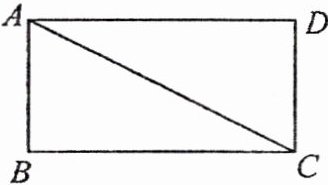
9. (2022·山西)如图, 在矩形 $ABCD$ 中, $AC$ 是对角线.
(1) 实践与操作: 利用尺规作线段 $AC$ 的垂直平分线, 垂足为 $O$, 交边 $AD$ 于点 $E$, 交边 $BC$ 于点 $F$ (要求: 尺规作图并保留作图痕迹, 不写作法, 标明字母).
(2) 猜想与证明: 试猜想线段 $AE$ 与 $CF$ 的数量关系, 并加以证明.
(1) 实践与操作: 利用尺规作线段 $AC$ 的垂直平分线, 垂足为 $O$, 交边 $AD$ 于点 $E$, 交边 $BC$ 于点 $F$ (要求: 尺规作图并保留作图痕迹, 不写作法, 标明字母).
(2) 猜想与证明: 试猜想线段 $AE$ 与 $CF$ 的数量关系, 并加以证明.

答案:
9.解:
(1)
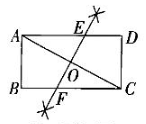
(2)$AE = CF$。证明:$\because$四边形$ABCD$是矩形,$\therefore AD // BC$,$\therefore \angle EAO = \angle FCO$,$\angle AEO = \angle CFO$。$\because EF$是$AC$的垂直平分线,$\therefore \angle AEO = \angle CFO$,$AO = CO$。在$\triangle AOE$和$\triangle COF$中,$\begin{cases} \angle EAO = \angle FCO, \\ AO = CO, \\ \angle AOE = \angle COF \end{cases} \therefore \triangle AOE \cong \triangle COF (AAS)$,$\therefore AE = CF$。
9.解:
(1)

(2)$AE = CF$。证明:$\because$四边形$ABCD$是矩形,$\therefore AD // BC$,$\therefore \angle EAO = \angle FCO$,$\angle AEO = \angle CFO$。$\because EF$是$AC$的垂直平分线,$\therefore \angle AEO = \angle CFO$,$AO = CO$。在$\triangle AOE$和$\triangle COF$中,$\begin{cases} \angle EAO = \angle FCO, \\ AO = CO, \\ \angle AOE = \angle COF \end{cases} \therefore \triangle AOE \cong \triangle COF (AAS)$,$\therefore AE = CF$。
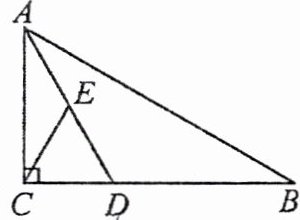
10. (2023·太原成成中学期末)如图, 在 $Rt\triangle ABC$ 中, $\angle ACB = 90^{\circ}$, $\angle B = 30^{\circ}$, $AD$ 平分 $\angle BAC$, $E$ 是 $AD$ 的中点. 若 $BD = 7$, 则 $CE$ 的长为 (
A.$3$
B.$3.5$
C.$4$
D.$4.5$
B
)
A.$3$
B.$3.5$
C.$4$
D.$4.5$
答案:
10.B
11. 一个四边形顺次添加下列条件中的三个条件便得到正方形:
a. 两组对边分别相等; b. 一组对边平行且相等; c. 一组邻边相等; d. 一个角是直角. 顺次添加的条件: ① $a \to c \to d$; ② $b \to d \to c$; ③ $a \to b \to c$.

则正确的是 (
A.仅①
B.仅③
C.①②
D.②③
a. 两组对边分别相等; b. 一组对边平行且相等; c. 一组邻边相等; d. 一个角是直角. 顺次添加的条件: ① $a \to c \to d$; ② $b \to d \to c$; ③ $a \to b \to c$.

则正确的是 (
C
)A.仅①
B.仅③
C.①②
D.②③
答案:
11.C
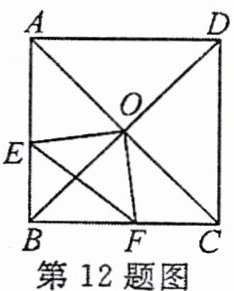
12. (2024·忻州忻府区期中)如图所示, 在正方形 $ABCD$ 中, $O$ 是对角线 $AC$, $BD$ 的交点, 过点 $O$ 作 $OE \perp OF$, 分别交 $AB$, $BC$ 于点 $E$, $F$. 若 $AE = 4$, $CF = 3$, 则 $EF$ 的长为 (
A.$3$
B.$4$
C.$5$
D.$6$
C
)
A.$3$
B.$4$
C.$5$
D.$6$
答案:
12.C
13. 新考向 真实情境 (2024·朔州右玉县二模)图 1 是某创意图书馆设计的一款壁灯图案的设计图, 象征着欣欣向荣, 代表一种生机盎然的自然和谐美. 图 2 是从图 1 所示的图案中提取的图形, 已知正八边形 $ABCDEFGH$ 被分割成两个正方形和四个菱形, 则 $\angle JIK =$ ________.
]

]

答案:
13.$45°$
14. 综合与实践:
宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ (约为 $0.618$) 的矩形叫黄金矩形. 黄金矩形给我们以协调、匀称的美感, 世界各国许多著名的建筑, 为取得最佳的视觉效果, 都采用黄金矩形的设计, 如希腊的帕特农神庙等.
实践操作: 下面我们折叠出一个黄金矩形 (如图所示).
第一步: 在一张矩形纸片的一端, 利用图 1 的方法折出一个正方形, 然后把纸展平.
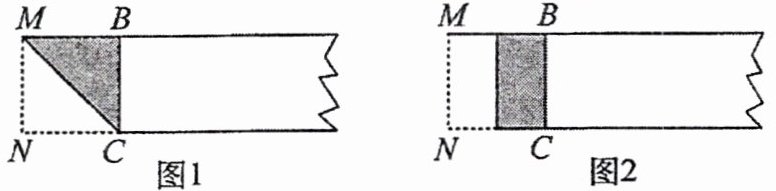
第二步: 如图 2, 把这个正方形折成两个相等的矩形, 再把纸片展平.
第三步: 折出内侧矩形的对角线 $AB$, 并把 $AB$ 折到如图 3 所示的 $AD$ 处.
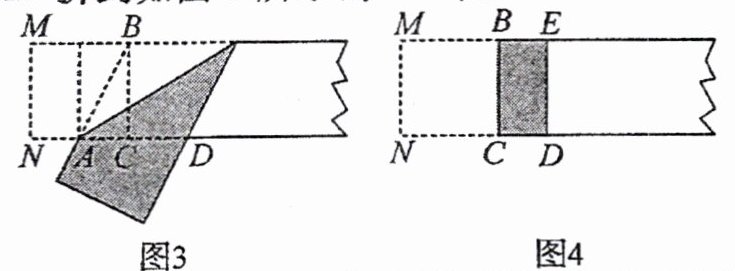
第四步: 展平纸片, 按照所得的点 $D$ 折出 $DE$, 则矩形 $BCDE$ (图 4) 就是黄金矩形.
问题解决:
(1) 请在图 1 中证明四边形 $MNBC$ 是正方形.
(2) 若 $MN = 4$, 请通过计算 $\frac{BE}{BC}$ 的值来说明矩形 $BCDE$ 是黄金矩形.
宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ (约为 $0.618$) 的矩形叫黄金矩形. 黄金矩形给我们以协调、匀称的美感, 世界各国许多著名的建筑, 为取得最佳的视觉效果, 都采用黄金矩形的设计, 如希腊的帕特农神庙等.
实践操作: 下面我们折叠出一个黄金矩形 (如图所示).
第一步: 在一张矩形纸片的一端, 利用图 1 的方法折出一个正方形, 然后把纸展平.

第二步: 如图 2, 把这个正方形折成两个相等的矩形, 再把纸片展平.
第三步: 折出内侧矩形的对角线 $AB$, 并把 $AB$ 折到如图 3 所示的 $AD$ 处.

第四步: 展平纸片, 按照所得的点 $D$ 折出 $DE$, 则矩形 $BCDE$ (图 4) 就是黄金矩形.
问题解决:
(1) 请在图 1 中证明四边形 $MNBC$ 是正方形.
(2) 若 $MN = 4$, 请通过计算 $\frac{BE}{BC}$ 的值来说明矩形 $BCDE$ 是黄金矩形.
答案:
14.解:
(1)证明:由矩形的性质可知,$\angle BMN = \angle N = 90°$,由折叠可知,$\angle MBC = \angle N = 90°$,$MN = MB$,$\therefore \angle BMN = \angle N = \angle MBC = 90°$,$\therefore$四边形$MNCB$是矩形。又$\because MN = MB$,$\therefore$矩形$MNCB$是正方形。
(2)$\because MN = 4$,$\therefore NC = BC = MN = 4$,$\therefore AC = \frac{1}{2}NC = 2$。在$Rt \triangle ABC$中,$AB = \sqrt{AC^2 + BC^2} = \sqrt{2^2 + 4^2} = 2\sqrt{5}$。由折叠可知,$AD = AB = 2\sqrt{5}$,$\therefore BE = CD = AD - AC = 2\sqrt{5} - 2$,$\therefore \frac{BE}{BC} = \frac{2\sqrt{5} - 2}{4} = \frac{\sqrt{5} - 1}{2}$,$\therefore$矩形$BCDE$是黄金矩形。
(1)证明:由矩形的性质可知,$\angle BMN = \angle N = 90°$,由折叠可知,$\angle MBC = \angle N = 90°$,$MN = MB$,$\therefore \angle BMN = \angle N = \angle MBC = 90°$,$\therefore$四边形$MNCB$是矩形。又$\because MN = MB$,$\therefore$矩形$MNCB$是正方形。
(2)$\because MN = 4$,$\therefore NC = BC = MN = 4$,$\therefore AC = \frac{1}{2}NC = 2$。在$Rt \triangle ABC$中,$AB = \sqrt{AC^2 + BC^2} = \sqrt{2^2 + 4^2} = 2\sqrt{5}$。由折叠可知,$AD = AB = 2\sqrt{5}$,$\therefore BE = CD = AD - AC = 2\sqrt{5} - 2$,$\therefore \frac{BE}{BC} = \frac{2\sqrt{5} - 2}{4} = \frac{\sqrt{5} - 1}{2}$,$\therefore$矩形$BCDE$是黄金矩形。
查看更多完整答案,请扫码查看


