《2025年名校课堂九年级数学上册北师大版山西专版》

8. 已知一个两位数等于其各数位上数字的积的3倍，且个位数字比十位数字大2，则这个两位数是24.

答案： 8.24

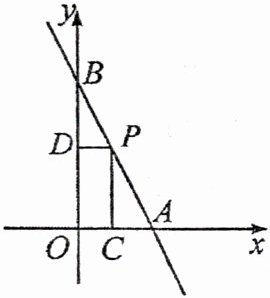
9. (教材P58复习题T20变式)如图，一次函数y=-2x+6的图象交x轴于点A，交y轴于点B，点P在线段AB上(不与点A，B重合)，过点P分别作OA和OB的垂线，垂足为C，D.当矩形OCPD的面积为4时，点P的坐标为(1,4)或(2,2).

答案： 9.(1,4)或(2,2)

10. (教材P52引言变式)如图，一个长为15 m的梯子斜靠在墙上，梯子的顶端距地面的距离OA为12 m，梯子的顶端从A处沿墙AO下滑的距离与点B向外移动的距离可能相等吗？若可能，请求出这个距离；若不可能，请说明理由.

答案： 10.解：假设梯子的顶端从$A$处沿墙$AO$下滑的距离与点$B$向外移动的距离相等，且这个距离为$x$m，即$AA'=BB'=x$m.在$Rt\triangle AOB$中，$OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{15^{2}-12^{2}}=9(m)$.则$OA'=(12-x)m$，$OB'=(9+x)m$.在$Rt\triangle A'OB'$中，根据勾股定理，得$OA'^{2}+OB'^{2}=A'B'^{2}$，$\therefore(12-x)^{2}+(9+x)^{2}=15^{2}$，解得$x_1=0$(舍去)，$x_2=3$.答：梯子的顶端从$A$处沿墙$AO$下滑的距离与点$B$向外移动的距离可能相等，且这个距离是3m.

11. (教材P57复习题T18变式)如图，已知一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20√{10}海里的圆形区域(包括边界)都属于台风区.当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里.若这艘轮船自A处按原速度继续航行，在途中会不会遇到台风？若会，试求轮船最初遇到台风的时间；若不会，请说明理由.

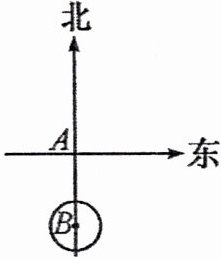
答案： 11.解：假设途中会遇到台风，且最初遇到的时间为$t$h，此时轮船位于$C$处，台风中心移到$E$处，连接$CE$，则$AC=20t$，$AE=AB-BE=100-40t$，$CE=20\sqrt{10}$.在$Rt\triangle ACE$中，根据勾股定理，得$AC^{2}+AE^{2}=EC^{2}.\therefore(20t)^{2}+(100-40t)^{2}=(20\sqrt{10})^{2}$.解得$t_1=1$，$t_2=3$(不合题意，舍去).答：这艘轮船自$A$处按原速度继续航行，在途中会遇到台风，且轮船最初遇到台风的时间为从$A$处出发后1h.

12. 如图，在矩形ABCD中，AB=5 cm，BC=6 cm，点P从点A开始，沿边AB向终点B以1 cm/s的速度移动，与此同时，点Q从点B开始，沿边BC向终点C以2 cm/s的速度移动.如果点P，Q分别从点A，B同时出发，当点Q运动到点C时，两点停止运动.设运动时间为t s.
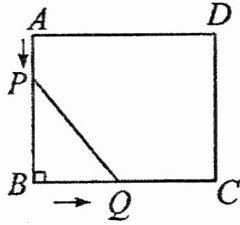
(1)填空：BQ=2tcm，PB=(5-t)cm(用含t的代数式表示).
(2)当t为何值时，PQ的长度等于5 cm？
(3)是否存在t的值，使得五边形APQCD的面积等于26 cm²？若存在，请求出此时t的值；若不存在，请说明理由.

答案： 12.解：
(1)$2t(5-t)$
(2)根据题意，得$(5-t)^{2}+(2t)^{2}=5^{2}$，解得$t_1=0$，$t_2=2$.故当$t=0$或$2$时，$PQ$的长度等于$5$cm.
(3)存在，当$t=1$时，五边形$APQCD$的面积等于$26cm^2$.理由如下：$\because S_{矩形ABCD}=5×6=30(cm^2)$，$S_{五边形APQCD}=26cm^2$，$\therefore S_{\triangle PBQ}=30-26=4(cm^2$).根据题意，得$\frac{1}{2}×(5-t)×2t=4$，解得$t_1=4$，$t_2=1$.当$t=4$时，$2t=8＞6$，故$t=4$不符合题意，舍去.故当$t=1$时，五边形$APQCD$的面积等于$26cm^2$.