2025年预习新初一
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年预习新初一 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第121页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
练3-1 如图,OC平分∠AOB,OD,OE三等分∠AOB,已知∠COE = 15°,求∠AOB的度数.
解:因为OC平分∠AOB,
所以∠BOC=
因为OD,OE三等分∠AOB,
所以∠BOE=
所以∠COE=∠BOC-∠BOE
=
=
所以∠AOB=6∠COE=6×15°=
解:因为OC平分∠AOB,
所以∠BOC=
$\frac{1}{2}∠AOB$
.因为OD,OE三等分∠AOB,
所以∠BOE=
$\frac{1}{3}∠AOB$
.所以∠COE=∠BOC-∠BOE
=
$\frac{1}{2}∠AOB$
-$\frac{1}{3}∠AOB$
=
$\frac{1}{6}∠AOB$
.所以∠AOB=6∠COE=6×15°=
90°
.
答案:
练3-1 解:因为OC平分$∠AOB$,
所以$∠BOC=\frac {1}{2}∠AOB$.
因为OD,OE三等分$∠AOB$,
所以$∠BOE=\frac {1}{3}∠AOB$.
所以$∠COE=∠BOC-∠BOE$
$=\frac {1}{2}∠AOB-\frac {1}{3}∠AOB$
$=\frac {1}{6}∠AOB$.
所以$∠AOB=6∠COE=6×15^{\circ }=90^{\circ }$.
所以$∠BOC=\frac {1}{2}∠AOB$.
因为OD,OE三等分$∠AOB$,
所以$∠BOE=\frac {1}{3}∠AOB$.
所以$∠COE=∠BOC-∠BOE$
$=\frac {1}{2}∠AOB-\frac {1}{3}∠AOB$
$=\frac {1}{6}∠AOB$.
所以$∠AOB=6∠COE=6×15^{\circ }=90^{\circ }$.
1.如图,在边长相等的正方形网格中,∠1与∠2的大小关系为 (
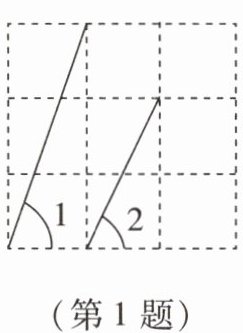
A.∠1 > ∠2
B.∠1 = ∠2
C.∠1 < ∠2
D.无法确定
A
)
A.∠1 > ∠2
B.∠1 = ∠2
C.∠1 < ∠2
D.无法确定
答案:
1. A
2.比较∠CAB与∠DAB的大小时,把它们的顶点A和边AB重合,把它们的另一边AC和AD放在AB的同一侧,若∠CAB > ∠DAB,则 (
A.AD落在∠CAB的内部
B.AD落在∠CAB的外部
C.AC和AD重合
D.不能确定AD的位置
A
)A.AD落在∠CAB的内部
B.AD落在∠CAB的外部
C.AC和AD重合
D.不能确定AD的位置
答案:
2. A
3.亮亮在综合实践课中学习三角板的相关知识,如图,他将一个三角板60°角的顶点与另一个三角板的直角顶点重合,若此时∠1 = 27°,则∠2的度数是 (
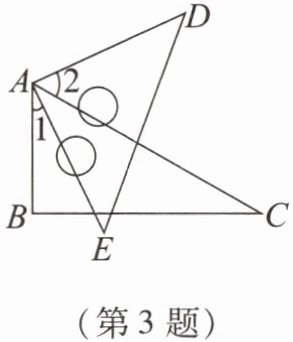
A.63°
B.57°
C.33°
D.27°
B
)
A.63°
B.57°
C.33°
D.27°
答案:
3. B
4.如图,∠AOB是平角,OC是射线,OD,OE分别是∠AOC,∠BOC的平分线,若∠BOE = 30°26',则∠COD的度数为 (
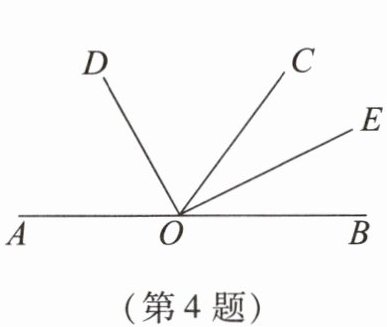
A.31°26'
B.59°34'
C.68°16'
D.68°34'
B
)
A.31°26'
B.59°34'
C.68°16'
D.68°34'
答案:
4. B
5.如图,直线m外有一定点O,A是m上的一个动点,当点A从左向右运动时,观察∠α的变化情况,正确的是 (
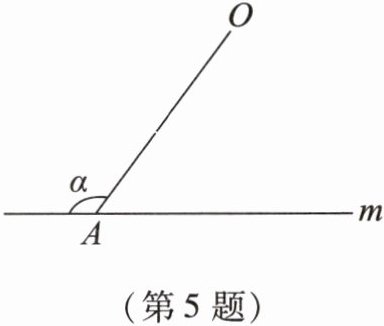
A.逐渐变小
B.逐渐变大
C.大小不变
D.无法确定
A
)
A.逐渐变小
B.逐渐变大
C.大小不变
D.无法确定
答案:
5. A
6.计算:
(1)153°29'42'' + 26°40'32'';
(2)62°24'17'' × 4.
(1)153°29'42'' + 26°40'32'';
(2)62°24'17'' × 4.
答案:
$(1)$计算$153^{\circ}29'42'' + 26^{\circ}40'32''$
解:
根据度、分、秒之间的换算关系:$1^{\circ}=60'$,$1' = 60''$,将度与度、分与分、秒与秒分别相加:
秒:$42''+32'' = 74''$,因为$74''=60'' + 14''$,所以$74'' = 1'14''$;
分:$29'+40'+1'=70'$,又因为$70'=60'+10'$,所以$70' = 1^{\circ}10'$;
度:$153^{\circ}+26^{\circ}+1^{\circ}=180^{\circ}$。
所以$153^{\circ}29'42'' + 26^{\circ}40'32''=180^{\circ}10'14''$。
$(2)$计算$62^{\circ}24'17''×4$
解:
根据乘法分配律$(a + b + c)× d=ad+bd+cd$(这里$a = 62^{\circ}$,$b = 24'$,$c = 17''$,$d = 4$):
度:$62^{\circ}×4=248^{\circ}$;
分:$24'×4 = 96'$,由于$96'=60'+36'$,即$96' = 1^{\circ}36'$;
秒:$17''×4=68''$,因为$68''=60'' + 8''$,所以$68'' = 1'8''$。
然后将结果相加:$248^{\circ}+1^{\circ}+36'+1'+8''=249^{\circ}37'8''$。
综上,答案依次为:$(1)$$\boldsymbol{180^{\circ}10'14''}$;$(2)$$\boldsymbol{249^{\circ}37'8''}$。
解:
根据度、分、秒之间的换算关系:$1^{\circ}=60'$,$1' = 60''$,将度与度、分与分、秒与秒分别相加:
秒:$42''+32'' = 74''$,因为$74''=60'' + 14''$,所以$74'' = 1'14''$;
分:$29'+40'+1'=70'$,又因为$70'=60'+10'$,所以$70' = 1^{\circ}10'$;
度:$153^{\circ}+26^{\circ}+1^{\circ}=180^{\circ}$。
所以$153^{\circ}29'42'' + 26^{\circ}40'32''=180^{\circ}10'14''$。
$(2)$计算$62^{\circ}24'17''×4$
解:
根据乘法分配律$(a + b + c)× d=ad+bd+cd$(这里$a = 62^{\circ}$,$b = 24'$,$c = 17''$,$d = 4$):
度:$62^{\circ}×4=248^{\circ}$;
分:$24'×4 = 96'$,由于$96'=60'+36'$,即$96' = 1^{\circ}36'$;
秒:$17''×4=68''$,因为$68''=60'' + 8''$,所以$68'' = 1'8''$。
然后将结果相加:$248^{\circ}+1^{\circ}+36'+1'+8''=249^{\circ}37'8''$。
综上,答案依次为:$(1)$$\boldsymbol{180^{\circ}10'14''}$;$(2)$$\boldsymbol{249^{\circ}37'8''}$。
查看更多完整答案,请扫码查看


