《2025年阳光假日暑假六年级数学人教版》

六、用下面的数字卡片按要求组数。

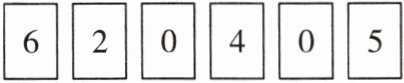
最大的六位数: 654200。
最小的六位数: 200456。
只读一个零的六位数: 620450（答案不唯一）。
两个零都读的六位数: 620405（答案不唯一）。
一个零也不读的六位数: 624500（答案不唯一）。

答案： 【解析】：
- 要组成最大的六位数，就把这六个数字从大到小排列，得到$654200$。
- 要组成最小的六位数，因为$0$不能在最高位，所以把除$0$外最小的数字$2$放在最高位，然后把剩下的数字从小到大排列（$0$放在次高位等合适位置），得到$200456$。
- 只读一个零的六位数，根据整数的读法，每一级末尾的$0$都不读出来，其余数位连续几个$0$都只读一个零，例如$620450$（答案不唯一）。
- 两个零都读的六位数，例如$620405$（答案不唯一）。
- 一个零也不读的六位数，把$0$放在每级的末尾，例如$624500$（答案不唯一）。
【答案】：
最大的六位数:$654200$。
最小的六位数:$200456$。
只读一个零的六位数:$620450$（答案不唯一）。
两个零都读的六位数:$620405$（答案不唯一）。
一个零也不读的六位数:$624500$（答案不唯一）。

七、猜一猜。
有一个五位数,最低位上的数字是 8,最高位上的数字是十位上数字的 4 倍,前三位数的和与后三位数的和都是 19,这个五位数是多少?

答案： 【解析】：已知这个五位数最低位（个位）上的数字是$8$。设十位上的数字为$x$，因为最高位（万位）上的数字是十位上数字的$4$倍，则万位上的数字为$4x$。由于一个数位上的数字只能是$0 - 9$的整数，所以$x$只能为$1$或$2$，当$x = 1$时，万位数字$4x=4$；当$x = 2$时，万位数字$4x = 8$。
又因为后三位（个位、十位、百位）数字的和是$19$，个位是$8$，设百位数字为$y$，若十位$x = 1$，则$8 + 1+y=19$，解得$y = 10$，不符合一个数位上数字的范围；若十位$x = 2$，则$8 + 2+y=19$，解得$y = 9$，符合要求，所以十位数字是$2$，万位数字是$8$，百位数字是$9$。
因为前三位（万位、千位、百位）数字的和是$19$，万位是$8$，百位是$9$，设千位数字为$z$，则$8+z + 9=19$，解得$z = 2$。
综上，这个五位数是$82928$。
【答案】：$82928$

1. 小龙的爸爸向银行贷了一笔款,两年归还,贷款年利率为 6%(不计复利)。他用这笔款购进一批货物,以高于买入价的 37%出售,经过两年的时间售完,用所得收入还清贷款本利,还剩 4 万元。那么两年前小龙的爸爸贷款的金额是多少万元?

答案： 【解析】：设两年前小龙的爸爸贷款的金额是$x$万元。
贷款两年后的本利和为$x + x\times6\%\times2=x(1 + 0.12)=1.12x$万元。
货物出售后的收入为$(1 + 37\%)x = 1.37x$万元。
已知用所得收入还清贷款本利后还剩$4$万元，则可列出方程：
$1.37x-1.12x = 4$
$0.25x = 4$
解得$x = 16$。
【答案】：$16$