《2025年阳光假日暑假六年级数学人教版》

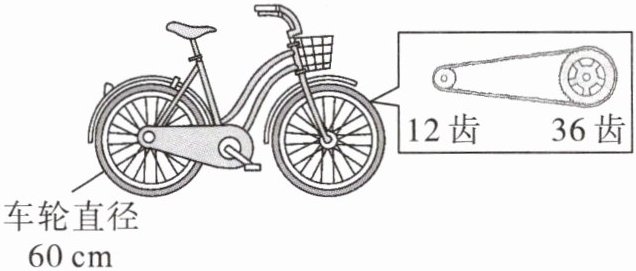
1. 这辆自行车蹬一圈能走多少米?($π$取3)

5.4

答案： 【解析】：
- 首先分析前后齿轮的关系：
因为在骑自行车时，前齿轮转一圈，后齿轮会转的圈数$n=\frac{前齿轮齿数}{后齿轮齿数}$。已知前齿轮$36$齿，后齿轮$12$齿，所以后齿轮转的圈数$n = \frac{36}{12}=3$圈。
而后齿轮与车轮是同步转动的，即车轮也转$3$圈。
然后计算车轮的周长：
已知车轮直径$d = 60cm$，根据圆的周长公式$C=\pi d$（$\pi$取$3$），可得车轮周长$C = 3\times60=180cm$。
最后计算蹬一圈自行车走的距离：
因为车轮转$3$圈，所以蹬一圈自行车走的距离$s = 3\times C$。把$C = 180cm$代入，可得$s=3\times180 = 540cm$。
因为$1m=100cm$，所以$540cm = 5.4m$。
【答案】：$5.4$

2. 皮皮新买了一辆变速自行车,前齿轮齿数分别为38、28,后齿轮齿数分别为24、20、18、16、14。
(1) 这辆自行车有多少种不同的组合?
(2) 蹬一圈,哪种组合最省力?
(3) 如果车轮直径为50cm,那么用最省力组合过一座长314m的桥,至少要蹬多少圈?(得数保留整数)

答案： 【解析】：
(1) 前齿轮有$2$种选择，后齿轮有$5$种选择，根据乘法原理，不同的组合数为前齿轮的种数乘以后齿轮的种数，即$2\times5 = 10$种。
(2) 蹬一圈，自行车前进的距离与前后齿轮的齿数比有关，齿数比越小越省力。分别计算出各种组合的齿数比：
前齿轮$38$，后齿轮$24$时，齿数比为$38\div24=\frac{19}{12}\approx1.58$；
前齿轮$38$，后齿轮$20$时，齿数比为$38\div20 = 1.9$；
前齿轮$38$，后齿轮$18$时，齿数比为$38\div18=\frac{19}{9}\approx2.11$；
前齿轮$38$，后齿轮$16$时，齿数比为$38\div16=\frac{19}{8}=2.375$；
前齿轮$38$，后齿轮$14$时，齿数比为$38\div14=\frac{19}{7}\approx2.71$；
前齿轮$28$，后齿轮$24$时，齿数比为$28\div24=\frac{7}{6}\approx1.17$；
前齿轮$28$，后齿轮$20$时，齿数比为$28\div20 = 1.4$；
前齿轮$28$，后齿轮$18$时，齿数比为$28\div18=\frac{14}{9}\approx1.56$；
前齿轮$28$，后齿轮$16$时，齿数比为$28\div16=\frac{7}{4}=1.75$；
前齿轮$28$，后齿轮$14$时，齿数比为$28\div14 = 2$。
比较可得，前齿轮$28$，后齿轮$24$的齿数比最小，所以这种组合最省力。
(3) 先根据圆的周长公式$C=\pi d$（$d$为直径）求出车轮的周长，$d = 50cm=0.5m$，则车轮周长$C = 3.14\times0.5 = 1.57m$。
最省力组合的齿数比为$\frac{7}{6}$，即蹬一圈，车轮转$\frac{7}{6}$圈，那么蹬一圈自行车前进的距离为$1.57\times\frac{7}{6}$米。
桥长$314m$，则至少要蹬的圈数为$314\div(1.57\times\frac{7}{6})$
$=314\div1.57\div\frac{7}{6}$
$=200\times\frac{6}{7}$
$=\frac{1200}{7}\approx171.43$，因为圈数需保留整数，所以至少要蹬$172$圈。
【答案】：
(1) $10$种；
(2) 前齿轮$28$，后齿轮$24$；
(3) $172$圈