第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 制作5节圆柱形通风管,每节长1m,底面半径是10cm,至少需要(
A. 0.628
B. 3.14
C. 6.28
D. 31.4
B
)$m^{2}$的铁皮。A. 0.628
B. 3.14
C. 6.28
D. 31.4
答案:
B
2. 一个圆柱的侧面展开图是一个正方形。这个圆柱的底面直径与高的比是(
A. $1:π$
B. $1:2π$
C. $1:4π$
D. $2:π$
A
)。A. $1:π$
B. $1:2π$
C. $1:4π$
D. $2:π$
答案:
A
3. 一个圆柱的底面周长是31.4cm,如果高增加2cm,底面大小不变,那么表面积增加了(
A. 15.7
B. 31.4
C. 62.8
D. 125.6
C
)$cm^{2}$。A. 15.7
B. 31.4
C. 62.8
D. 125.6
答案:
C
三、下面是圆柱的有关数据,根据已知数据填表。
|底面直径/cm|高/cm|底面周长/cm|侧面积/$cm^{2}$|表面积/$cm^{2}$|
|----|----|----|----|----|
|0.8|2.4| | | |
| | |6.28|18.84| |
| |1|3.14| |4.71|
|底面直径/cm|高/cm|底面周长/cm|侧面积/$cm^{2}$|表面积/$cm^{2}$|
|----|----|----|----|----|
|0.8|2.4| | | |
| | |6.28|18.84| |
| |1|3.14| |4.71|
答案:
1. 对于第一行(底面直径$d = 0.8cm$,高$h=2.4cm$):
底面周长$C$:
根据公式$C=\pi d$,$\pi$取$3.14$,则$C = 3.14\times0.8=2.512cm$。
侧面积$S_{侧}$:
根据公式$S_{侧}=Ch$,$C = 2.512cm$,$h = 2.4cm$,则$S_{侧}=2.512\times2.4 = 6.0288cm^{2}$。
表面积$S_{表}$:
先求底面半径$r=\frac{d}{2}=\frac{0.8}{2}=0.4cm$,底面积$S_{底}=\pi r^{2}=3.14\times0.4^{2}=3.14\times0.16 = 0.5024cm^{2}$。
根据公式$S_{表}=S_{侧}+2S_{底}$,则$S_{表}=6.0288 + 2\times0.5024=6.0288 + 1.0048=7.0336cm^{2}$。
2. 对于第二行(底面周长$C = 6.28cm$,侧面积$S_{侧}=18.84cm^{2}$):
底面直径$d$:
根据公式$C=\pi d$,则$d=\frac{C}{\pi}$,$\pi$取$3.14$,$d=\frac{6.28}{3.14}=2cm$。
高$h$:
根据公式$S_{侧}=Ch$,则$h=\frac{S_{侧}}{C}$,$h=\frac{18.84}{6.28}=3cm$。
表面积$S_{表}$:
底面半径$r=\frac{d}{2}=\frac{2}{2}=1cm$,底面积$S_{底}=\pi r^{2}=3.14\times1^{2}=3.14cm^{2}$。
根据公式$S_{表}=S_{侧}+2S_{底}$,则$S_{表}=18.84+2\times3.14=18.84 + 6.28=25.12cm^{2}$。
3. 对于第三行(高$h = 1cm$,底面周长$C = 3.14cm$,表面积$S_{表}=4.71cm^{2}$):
底面直径$d$:
根据公式$C=\pi d$,$\pi$取$3.14$,则$d=\frac{C}{\pi}=\frac{3.14}{3.14}=1cm$。
侧面积$S_{侧}$:
根据公式$S_{侧}=Ch$,$C = 3.14cm$,$h = 1cm$,则$S_{侧}=3.14\times1=3.14cm^{2}$。
故表格从左到右,从上到下依次填:$2.512$,$6.0288$,$7.0336$;$2$,$3$,$25.12$;$1$,$3.14$。
底面周长$C$:
根据公式$C=\pi d$,$\pi$取$3.14$,则$C = 3.14\times0.8=2.512cm$。
侧面积$S_{侧}$:
根据公式$S_{侧}=Ch$,$C = 2.512cm$,$h = 2.4cm$,则$S_{侧}=2.512\times2.4 = 6.0288cm^{2}$。
表面积$S_{表}$:
先求底面半径$r=\frac{d}{2}=\frac{0.8}{2}=0.4cm$,底面积$S_{底}=\pi r^{2}=3.14\times0.4^{2}=3.14\times0.16 = 0.5024cm^{2}$。
根据公式$S_{表}=S_{侧}+2S_{底}$,则$S_{表}=6.0288 + 2\times0.5024=6.0288 + 1.0048=7.0336cm^{2}$。
2. 对于第二行(底面周长$C = 6.28cm$,侧面积$S_{侧}=18.84cm^{2}$):
底面直径$d$:
根据公式$C=\pi d$,则$d=\frac{C}{\pi}$,$\pi$取$3.14$,$d=\frac{6.28}{3.14}=2cm$。
高$h$:
根据公式$S_{侧}=Ch$,则$h=\frac{S_{侧}}{C}$,$h=\frac{18.84}{6.28}=3cm$。
表面积$S_{表}$:
底面半径$r=\frac{d}{2}=\frac{2}{2}=1cm$,底面积$S_{底}=\pi r^{2}=3.14\times1^{2}=3.14cm^{2}$。
根据公式$S_{表}=S_{侧}+2S_{底}$,则$S_{表}=18.84+2\times3.14=18.84 + 6.28=25.12cm^{2}$。
3. 对于第三行(高$h = 1cm$,底面周长$C = 3.14cm$,表面积$S_{表}=4.71cm^{2}$):
底面直径$d$:
根据公式$C=\pi d$,$\pi$取$3.14$,则$d=\frac{C}{\pi}=\frac{3.14}{3.14}=1cm$。
侧面积$S_{侧}$:
根据公式$S_{侧}=Ch$,$C = 3.14cm$,$h = 1cm$,则$S_{侧}=3.14\times1=3.14cm^{2}$。
故表格从左到右,从上到下依次填:$2.512$,$6.0288$,$7.0336$;$2$,$3$,$25.12$;$1$,$3.14$。
四、求下面圆柱的表面积。(单位:cm)
1.
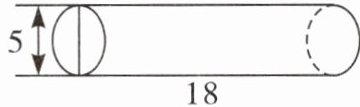
(
2.
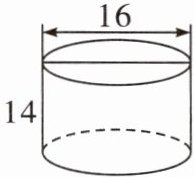
(
1.

(
321.85cm²
)2.

(
1105.28cm²
)
答案:
【解析】:
1. 先求底面半径$r = 5\div2 = 2.5$(cm),底面积$S_{底}=\pi r^{2}=3.14\times2.5^{2}=19.625$($cm^{2}$),侧面积$S_{侧}=\pi dh = 3.14\times5\times18 = 282.6$($cm^{2}$),表面积$S = 2S_{底}+S_{侧}=2\times19.625 + 282.6 = 39.25 + 282.6 = 321.85$($cm^{2}$)。
2. 先求底面半径$r = 16\div2 = 8$(cm),底面积$S_{底}=\pi r^{2}=3.14\times8^{2}=200.96$($cm^{2}$),侧面积$S_{侧}=\pi dh = 3.14\times16\times14 = 703.36$($cm^{2}$),表面积$S = 2S_{底}+S_{侧}=2\times200.96 + 703.36 = 401.92 + 703.36 = 1105.28$($cm^{2}$)。
【答案】:
1. $321.85cm^{2}$
2. $1105.28cm^{2}$
1. 先求底面半径$r = 5\div2 = 2.5$(cm),底面积$S_{底}=\pi r^{2}=3.14\times2.5^{2}=19.625$($cm^{2}$),侧面积$S_{侧}=\pi dh = 3.14\times5\times18 = 282.6$($cm^{2}$),表面积$S = 2S_{底}+S_{侧}=2\times19.625 + 282.6 = 39.25 + 282.6 = 321.85$($cm^{2}$)。
2. 先求底面半径$r = 16\div2 = 8$(cm),底面积$S_{底}=\pi r^{2}=3.14\times8^{2}=200.96$($cm^{2}$),侧面积$S_{侧}=\pi dh = 3.14\times16\times14 = 703.36$($cm^{2}$),表面积$S = 2S_{底}+S_{侧}=2\times200.96 + 703.36 = 401.92 + 703.36 = 1105.28$($cm^{2}$)。
【答案】:
1. $321.85cm^{2}$
2. $1105.28cm^{2}$
查看更多完整答案,请扫码查看


