《2025年阳光假日暑假六年级数学人教版》

5. 在一幅地图上,测得甲、乙两地的图上距离是13cm,已知甲、乙两地的实际距离是780km。在这幅地图上量得A、B两地的图上距离是5cm,A、B两地的实际距离是多少千米?

答案： 【解析】：本题可先根据甲、乙两地的图上距离和实际距离求出这幅地图的比例尺，再根据比例尺和$A$、$B$两地的图上距离求出$A$、$B$两地的实际距离。
**步骤一：统一单位并求出这幅地图的比例尺**
因为$1km = 100000cm$，所以$780km = 780\times100000 = 78000000cm$。
根据比例尺$=$图上距离$:$实际距离，可得这幅地图的比例尺为$13:78000000 = 1:6000000$。
**步骤二：根据比例尺和$A$、$B$两地的图上距离求出$A$、$B$两地的实际距离**
已知$A$、$B$两地的图上距离是$5cm$，比例尺为$1:6000000$，根据实际距离$=$图上距离$\div$比例尺，可得$A$、$B$两地的实际距离为$5\div\frac{1}{6000000} = 5\times6000000 = 30000000cm$。
再将单位换算为千米，因为$1km = 100000cm$，所以$30000000cm = 30000000\div100000 = 300km$。
【答案】：$300$千米

6. 阳光社区新建的一个长方形健身广场长120m、宽60m,把它画在比例尺是1:6000的图纸上,图上长方形的周长是多少厘米?

答案： 【解析】：本题可先根据“图上距离 = 实际距离×比例尺”分别求出图上长方形的长和宽，再根据长方形周长公式计算出图上长方形的周长。
**步骤一：计算图上长方形的长和宽**
已知该健身广场实际长$120m$、宽$60m$，因为$1m = 100cm$，所以将长和宽的单位换算为厘米可得：$120m = 120\times100 = 12000cm$，$60m = 60\times100 = 6000cm$。
又已知该图纸的比例尺是$1:6000$，根据“图上距离 = 实际距离×比例尺”，分别计算图上长方形的长和宽：
图上长方形的长：$12000\times\frac{1}{6000} = 2cm$。
图上长方形的宽：$6000\times\frac{1}{6000} = 1cm$。
**步骤二：计算图上长方形的周长**
根据长方形的周长公式$C = (a + b)×2$（其中$C$表示周长，$a$表示长，$b$表示宽），将图上长方形的长$2cm$和宽$1cm$代入公式可得：
$(2 + 1)×2 = 3×2 = 6cm$。
【答案】：$6$

7. 把一块直角三角形钢板零件按1:200的比例尺画在图纸上。两条直角边实际一共长10.8m,它们的长度比是5:4。钢板零件在图纸上的面积是多少平方厘米?

答案： 【解析】：
本题可先根据两条直角边的实际总长度和长度比求出两条直角边的实际长度，再结合比例尺求出图上的长度，最后根据三角形面积公式求出图纸上的面积。
### 步骤一：求出两条直角边的实际长度
已知两条直角边实际一共长$10.8m$，它们的长度比是$5:4$，则可根据按比例分配的方法分别求出两条直角边的实际长度。
两条直角边的总份数为：$5 + 4 = 9$（份）
那么较长直角边的实际长度为：$10.8\times\frac{5}{9} = 6$（$m$）
较短直角边的实际长度为：$10.8\times\frac{4}{9} = 4.8$（$m$）
### 步骤二：根据比例尺求出两条直角边在图纸上的长度
因为比例尺是$1:200$，表示图上距离$1$厘米代表实际距离$200$厘米，$200$厘米$ = 2m$。
所以较长直角边在图纸上的长度为：$6\div2 = 3$（厘米）
较短直角边在图纸上的长度为：$4.8\div2 = 2.4$（厘米）
### 步骤三：计算钢板零件在图纸上的面积
根据三角形的面积公式$S = \frac{1}{2}ah$（其中$S$表示面积，$a$表示底，$h$表示高），可得该直角三角形在图纸上的面积为：
$\frac{1}{2}\times3\times2.4 = 3.6$（平方厘米）
【答案】：$3.6$平方厘米

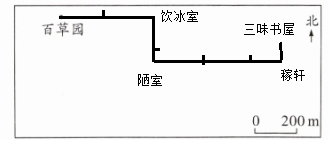
小贤从百草园出发,先向东走400m到达饮冰室,再向南走300m到达陋室,然后向东走500m到达稼轩,最后向北走100m到达三味书屋。在下图中画出小贤的行走路线,并标出各地点的位置。

答案：