第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
2. 如图,已知$AB = BC = CD = DE$。下面各组式子中,能组成比例的是(
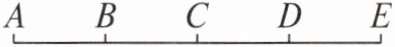
①$AB:AC$和$CD:CE$ ②$AD:AB$和$BE:DE$ ③$AD:CD$和$CE:DE$
A. ①②
B. ②③
C. ①③
D. ①②③
A
)。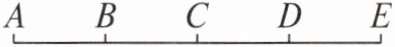
①$AB:AC$和$CD:CE$ ②$AD:AB$和$BE:DE$ ③$AD:CD$和$CE:DE$
A. ①②
B. ②③
C. ①③
D. ①②③
答案:
A
3. 如图,三角形$a$边上的高为$b$,$c$边上的高为$d$。根据这些信息,下面式子中,(
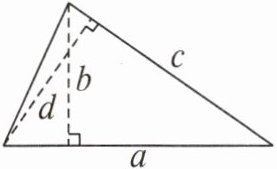
A. $a:c = d:b$
B. $a:c = b:d$
C. $\frac{a}{d}=\frac{c}{b}$
D. $\frac{b}{c}=\frac{d}{a}$
B
)不成立。
A. $a:c = d:b$
B. $a:c = b:d$
C. $\frac{a}{d}=\frac{c}{b}$
D. $\frac{b}{c}=\frac{d}{a}$
答案:
B
三、下面各表中相对应的两种量的比能否组成比例? 如果能,那么请把组成的比例写出来。
1.
|树高/m|6|9|
|----|----|----|
|影长/m|8|12|
2.
|圆的面积/dm²|12.56|78.5|
|----|----|----|
|圆的半径/dm|2|5|
1.
|树高/m|6|9|
|----|----|----|
|影长/m|8|12|
2.
|圆的面积/dm²|12.56|78.5|
|----|----|----|
|圆的半径/dm|2|5|
答案:
【解析】:
1. 对于第一组数据,判断两个比能否组成比例,要看它们的比值是否相等。树高与影长的比,$6:8=\frac{6}{8}=\frac{3}{4}$,$9:12 = \frac{9}{12}=\frac{3}{4}$,因为这两个比的比值相等,所以$6$、$8$、$9$、$12$能组成比例,组成的比例为$6:8 = 9:12$。
2. 对于第二组数据,圆的面积公式为$S=\pi r^{2}$,那么圆的面积与半径的比,$12.56:2=\frac{12.56}{2}=6.28$,$78.5:5=\frac{78.5}{5}=15.7$,这两个比的比值不相等,所以$12.56$、$2$、$78.5$、$5$不能组成比例。
【答案】:1. 能,$6:8 = 9:12$;2. 不能
1. 对于第一组数据,判断两个比能否组成比例,要看它们的比值是否相等。树高与影长的比,$6:8=\frac{6}{8}=\frac{3}{4}$,$9:12 = \frac{9}{12}=\frac{3}{4}$,因为这两个比的比值相等,所以$6$、$8$、$9$、$12$能组成比例,组成的比例为$6:8 = 9:12$。
2. 对于第二组数据,圆的面积公式为$S=\pi r^{2}$,那么圆的面积与半径的比,$12.56:2=\frac{12.56}{2}=6.28$,$78.5:5=\frac{78.5}{5}=15.7$,这两个比的比值不相等,所以$12.56$、$2$、$78.5$、$5$不能组成比例。
【答案】:1. 能,$6:8 = 9:12$;2. 不能
四、应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
$0.6:0.9$和$9:12$ $0.3:0.5$和$21:35$
$\frac{4}{5}:36$和$0.2:80$ $24:15$和$16:10$
$0.6:0.9$和$9:12$ $0.3:0.5$和$21:35$
$\frac{4}{5}:36$和$0.2:80$ $24:15$和$16:10$
答案:
【解析】:比例的基本性质是:在比例里,两个外项的积等于两个内项的积。
- 对于$0.6:0.9$和$9:12$,$0.6\times12 = 7.2$,$0.9\times9 = 8.1$,因为$7.2\neq8.1$,所以$0.6:0.9$和$9:12$不能组成比例。
- 对于$0.3:0.5$和$21:35$,$0.3\times35 = 10.5$,$0.5\times21 = 10.5$,因为$10.5 = 10.5$,所以$0.3:0.5$和$21:35$能组成比例。
- 对于$\frac{4}{5}:36$和$0.2:80$,$\frac{4}{5}\times80 = 64$,$36\times0.2 = 7.2$,因为$64\neq7.2$,所以$\frac{4}{5}:36$和$0.2:80$不能组成比例。
- 对于$24:15$和$16:10$,$24\times10 = 240$,$15\times16 = 240$,因为$240 = 240$,所以$24:15$和$16:10$能组成比例。
【答案】:$0.3:0.5$和$21:35$、$24:15$和$16:10$能组成比例;$0.6:0.9$和$9:12$、$\frac{4}{5}:36$和$0.2:80$不能组成比例。
- 对于$0.6:0.9$和$9:12$,$0.6\times12 = 7.2$,$0.9\times9 = 8.1$,因为$7.2\neq8.1$,所以$0.6:0.9$和$9:12$不能组成比例。
- 对于$0.3:0.5$和$21:35$,$0.3\times35 = 10.5$,$0.5\times21 = 10.5$,因为$10.5 = 10.5$,所以$0.3:0.5$和$21:35$能组成比例。
- 对于$\frac{4}{5}:36$和$0.2:80$,$\frac{4}{5}\times80 = 64$,$36\times0.2 = 7.2$,因为$64\neq7.2$,所以$\frac{4}{5}:36$和$0.2:80$不能组成比例。
- 对于$24:15$和$16:10$,$24\times10 = 240$,$15\times16 = 240$,因为$240 = 240$,所以$24:15$和$16:10$能组成比例。
【答案】:$0.3:0.5$和$21:35$、$24:15$和$16:10$能组成比例;$0.6:0.9$和$9:12$、$\frac{4}{5}:36$和$0.2:80$不能组成比例。
查看更多完整答案,请扫码查看


