第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
六、如图,在直线上有$A$、$B$、$C$三个点,请回答下列问题。
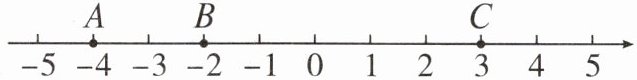
1. $A$、$C$两点间的距离是多少?
2. 若点$D$与点$B$之间的距离是$6$,写出点$D$表示的数。
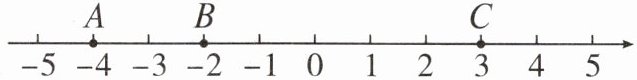
1. $A$、$C$两点间的距离是多少?
7
2. 若点$D$与点$B$之间的距离是$6$,写出点$D$表示的数。
4或-8
答案:
【解析】:
1. 计算$A$、$C$两点间的距离,用$C$点表示的数减去$A$点表示的数,即$3 - (-4)=3 + 4 = 7$。
2. 已知点$B$表示的数是$-2$,点$D$与点$B$之间的距离是$6$。
当点$D$在点$B$右侧时,点$D$表示的数为$-2 + 6 = 4$。
当点$D$在点$B$左侧时,点$D$表示的数为$-2 - 6 = -8$。
【答案】:
1. $7$
2. $4$或$-8$
1. 计算$A$、$C$两点间的距离,用$C$点表示的数减去$A$点表示的数,即$3 - (-4)=3 + 4 = 7$。
2. 已知点$B$表示的数是$-2$,点$D$与点$B$之间的距离是$6$。
当点$D$在点$B$右侧时,点$D$表示的数为$-2 + 6 = 4$。
当点$D$在点$B$左侧时,点$D$表示的数为$-2 - 6 = -8$。
【答案】:
1. $7$
2. $4$或$-8$
1. 六年级一名男生坚持每天进行一分钟跳绳锻炼。下表是他对自己一周的跳绳个数进行的统计,他将$150$个记为$0$,超出$150$个的部分用正数表示,不足$150$个的部分用负数表示。具体情况记录如下:

《国家学生体质健康标准》规定:六年级男生一分钟跳绳个数在$147$个以上(含$147$个)记为优秀,该男生这一周有(

《国家学生体质健康标准》规定:六年级男生一分钟跳绳个数在$147$个以上(含$147$个)记为优秀,该男生这一周有(
5
)次一分钟跳绳成绩为优秀。
答案:
【解析】:根据题意,将$150$个记为$0$,超出$150$个的部分用正数表示,不足$150$个的部分用负数表示,且六年级男生一分钟跳绳个数在$147$个以上(含$147$个)记为优秀。那么只要跳绳个数对应的记录数大于等于$-3$,其实际跳绳个数就大于等于$147$个,即为优秀。观察表格记录情况,找出大于等于$-3$的记录次数即可。
【答案】:$5$
【答案】:$5$
2. 已知直线上点$M$、$N$表示的数分别为$-3$、$1$,点$P$为直线上一点,其表示的数为$x$。直线上是否存在点$P$,使点$P$到点$M$、$N$的距离之和是$5$? 若存在,请直接写出$x$的值;若不存在,请说明理由。
答案:
解:根据两点间距离公式$\vert AB\vert=\vert a - b\vert$($A$表示数$a$,$B$表示数$b$),则点$P$到点$M$的距离为$\vert x - (-3)\vert=\vert x + 3\vert$,点$P$到点$N$的距离为$\vert x - 1\vert$。
已知点$P$到点$M$、$N$的距离之和是$5$,可得$\vert x + 3\vert+\vert x - 1\vert = 5$。
分三种情况讨论:
当$x\lt - 3$时,$x + 3\lt0$,$x - 1\lt0$,则$-(x + 3)-(x - 1)=5$,
即$-x - 3 - x + 1 = 5$,
$-2x-2 = 5$,
$-2x=5 + 2$,
$-2x=7$,
解得$x=-\dfrac{7}{2}$。
当$-3\leqslant x\leqslant1$时,$x + 3\geqslant0$,$x - 1\leqslant0$,则$(x + 3)-(x - 1)=5$,
即$x + 3 - x + 1 = 5$,
$4 = 5$,等式不成立,此情况无解。
当$x\gt1$时,$x + 3\gt0$,$x - 1\gt0$,则$(x + 3)+(x - 1)=5$,
即$x + 3 + x - 1 = 5$,
$2x+2 = 5$,
$2x=5 - 2$,
$2x=3$,
解得$x=\dfrac{3}{2}$。
综上,$x$的值为$-\dfrac{7}{2}$或$\dfrac{3}{2}$。
已知点$P$到点$M$、$N$的距离之和是$5$,可得$\vert x + 3\vert+\vert x - 1\vert = 5$。
分三种情况讨论:
当$x\lt - 3$时,$x + 3\lt0$,$x - 1\lt0$,则$-(x + 3)-(x - 1)=5$,
即$-x - 3 - x + 1 = 5$,
$-2x-2 = 5$,
$-2x=5 + 2$,
$-2x=7$,
解得$x=-\dfrac{7}{2}$。
当$-3\leqslant x\leqslant1$时,$x + 3\geqslant0$,$x - 1\leqslant0$,则$(x + 3)-(x - 1)=5$,
即$x + 3 - x + 1 = 5$,
$4 = 5$,等式不成立,此情况无解。
当$x\gt1$时,$x + 3\gt0$,$x - 1\gt0$,则$(x + 3)+(x - 1)=5$,
即$x + 3 + x - 1 = 5$,
$2x+2 = 5$,
$2x=5 - 2$,
$2x=3$,
解得$x=\dfrac{3}{2}$。
综上,$x$的值为$-\dfrac{7}{2}$或$\dfrac{3}{2}$。
查看更多完整答案,请扫码查看


