《2025年暑假衔接起跑线七升八数学浙教版》

例3 如图，长方形$ABCD$的边$AB=a$，$BC=b$，对角线$AC=c$，长方形$AB'C'D'$是一个与长方形$ABCD$完全相同的长方形，且点$B'$，$D'$分别在$DA$，$AB$的延长线上。请你利用梯形$B'C'CD$的面积证明$a^{2}+b^{2}=c^{2}$。
证明：因为长方形$AB'C'D'$与长方形$ABCD$完全相同，
所以$AB'=a$，$B'C'=b$，$AC'=c$，且$\angle D'AC'=\angle DAC$。
因为$\angle BAD=90^{\circ}$，所以$\angle BAC+\angle D'AC'=\angle BAC+\angle DAC=90^{\circ}$，即$\angle CAC'=90^{\circ}$，所以$S_{\triangle CAC'}=\frac{1}{2}c^{2}$，$S_{\triangle ACD}=S_{\triangle AB'C'}=\frac{1}{2}ab$，
所以$S_{梯形B'C'CD}=S_{\triangle CAC'}+S_{\triangle ACD}+S_{\triangle AB'C'}=\frac{1}{2}c^{2}+\frac{1}{2}ab+\frac{1}{2}ab=\frac{1}{2}c^{2}+ab$。
因为$\angle D=\angle B'=90^{\circ}$，所以$CD// B'C'$。
在梯形$B'C'CD$中，$S_{梯形B'C'CD}=\frac{1}{2}(CD+B'C')\cdot B'D=\frac{1}{2}(a+b)(a+b)=\frac{1}{2}(a^{2}+b^{2}+2ab)$。
所以$\frac{1}{2}c^{2}+ab$$=\frac{1}{2}(a^{2}+b^{2}+2ab)=\frac{1}{2}(a^{2}+b^{2})+ab$，
所以$c^{2}=a^{2}+b^{2}$。

答案： 证明：因为长方形$AB'C'D'$与长方形$ABCD$完全相同，
所以$AB'=a$，$B'C'=b$，$AC'=c$，且$\angle D'AC'=\angle DAC$。
因为$\angle BAD=90^{\circ}$，所以$\angle BAC+\angle D'AC'=\angle BAC+\angle DAC=90^{\circ}$，即$\angle CAC'=90^{\circ}$，所以$S_{\triangle CAC'}=\frac{1}{2}c^{2}$，$S_{\triangle ACD}=S_{\triangle AB'C'}=\frac{1}{2}ab$，
所以$S_{梯形B'C'CD}=S_{\triangle CAC'}+S_{\triangle ACD}+S_{\triangle AB'C'}=\frac{1}{2}c^{2}+\frac{1}{2}ab+\frac{1}{2}ab=\frac{1}{2}c^{2}+ab$。
因为$\angle D=\angle B'=90^{\circ}$，所以$CD// B'C'$。
在梯形$B'C'CD$中，$S_{梯形B'C'CD}=\frac{1}{2}(CD+B'C')\cdot B'D=\frac{1}{2}(a+b)(a+b)=\frac{1}{2}(a^{2}+b^{2}+2ab)$。
所以$\frac{1}{2}c^{2}+ab=\frac{1}{2}(a^{2}+b^{2}+2ab)=\frac{1}{2}(a^{2}+b^{2})+ab$，
所以$c^{2}=a^{2}+b^{2}$。

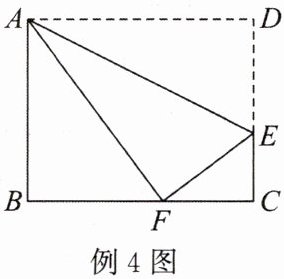
例4 如图，折叠长方形$ABCD$的一边$AD$，使点$D$落在$BC$边上的点$F$处，若$AB=8cm$，$BC=10cm$，求$EC$的长。

解：设$CE=$$x$$cm$，则$DE=$$(8-x)$$cm$。
因为$\triangle ADE$折叠后的图形为$\triangle AFE$，所以$\triangle ADE\cong\triangle AFE$，
所以$AF=AD=BC=$$10$$cm$，$EF=DE=$$(8-x)$$cm$。
在$Rt\triangle ABF$中，由勾股定理，得$BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{10^{2}-8^{2}}=$$6$$(cm)$。
所以$FC=10-6=$$4$$(cm)$。
在$Rt\triangle EFC$中，由勾股定理，得$EF^{2}=EC^{2}+FC^{2}$，
即$(8-x)^{2}=x^{2}+4^{2}$，解得$x=$$3$。即$EC$的长为$3$$cm$。

答案： 思路分析 本题依据条件“折叠长方形$ABCD$的一边$AD$，使点$D$落在$BC$边上的点$F$处”，可得$AF=AD=10cm$，$EF=DE=8-EC$。在$Rt\triangle ABF$中，由勾股定理可求出$BF$的长，便可知$FC$的长，然后在$Rt\triangle EFC$中，由勾股定理列方程即可求出$EC$的长。
解：设$CE=xcm$，则$DE=(8-x)cm$。
因为$\triangle ADE$折叠后的图形为$\triangle AFE$，所以$\triangle ADE\cong\triangle AFE$，
所以$AF=AD=BC=10cm$，$EF=DE=(8-x)cm$。
在$Rt\triangle ABF$中，由勾股定理，得$BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{10^{2}-8^{2}}=6(cm)$。
所以$FC=10-6=4(cm)$。
在$Rt\triangle EFC$中，由勾股定理，得$EF^{2}=EC^{2}+FC^{2}$，
即$(8-x)^{2}=x^{2}+4^{2}$，解得$x=3$。即$EC$的长为$3cm$。

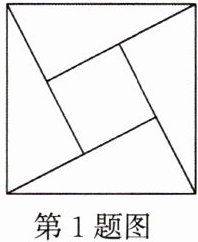
1. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲。如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形。设直角三角形较长直角边长为$a$，较短直角边长为$b$，若$(a+b)^{2}=21$，大正方形的面积为13，则小正方形的面积为（C）

A. 3
B. 4
C. 5
D. 6

答案： C