第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
21. 生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查。在为期半天的会议中,每人发一瓶$500$毫升的矿泉水,会后对所发矿泉水喝的情况进行统计,大致可分为四种:$A$. 全部喝完;$B$. 喝剩约$\frac{1}{3}$;$C$. 喝剩约一半;$D$. 开瓶但基本未喝。同学们根据统计结果绘制成下面的两幅统计图。根据统计图提供的信息,解答下列问题:
(1)参加这次会议的有多少人?图$2$中$D$所在扇形的圆心角是多少度?补全条形统计图;
(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费矿泉水约多少毫升?(计算结果请保留整数)
(3)据不完全统计,该单位每年约有$3000$人参加此类会议,请用(2)中的计算结果,估计该单位每年因此类会议浪费的矿泉水($500$毫升/瓶)约有多少瓶?(可使用科学计算器)
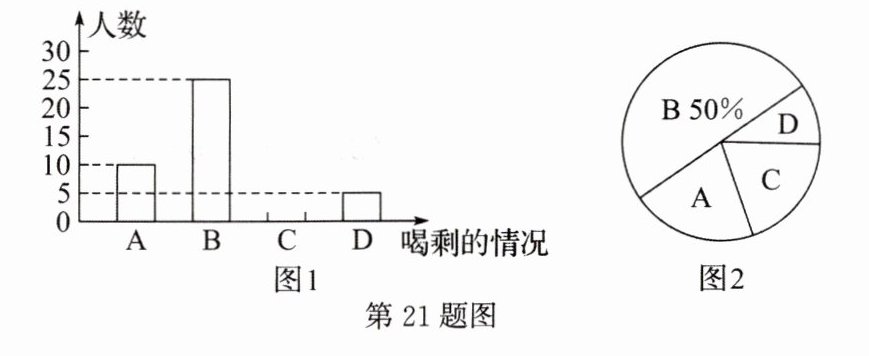
(1)参加这次会议的有多少人?图$2$中$D$所在扇形的圆心角是多少度?补全条形统计图;
(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费矿泉水约多少毫升?(计算结果请保留整数)
(3)据不完全统计,该单位每年约有$3000$人参加此类会议,请用(2)中的计算结果,估计该单位每年因此类会议浪费的矿泉水($500$毫升/瓶)约有多少瓶?(可使用科学计算器)

答案:
21. 解:
(1)参加这次会议的有 50 人。D 所在扇形圆心角的度数为$36^{\circ}$。补全条形统计图:
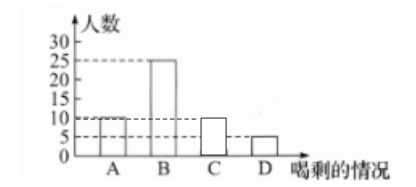
;
(2)平均每人浪费矿泉水量为 183 毫升;
(3)浪费的矿泉水约为 1098 瓶。
21. 解:
(1)参加这次会议的有 50 人。D 所在扇形圆心角的度数为$36^{\circ}$。补全条形统计图:

;
(2)平均每人浪费矿泉水量为 183 毫升;
(3)浪费的矿泉水约为 1098 瓶。
22. $2024$年春晚吉祥物“龙辰辰”,突出呈现吉祥如意、平安幸福的美好寓意,深受大家喜爱。某商店第一次用$3000$元购进一批“龙辰辰”玩具,很快售完;该商店第二次购进该“龙辰辰”玩具时,进价提高了$20\%$,同样用$3000$元购进的数量比第一次少了$10$件。
(1)求第一次购进的“龙辰辰”玩具每件的进价;
(2)若两次购进的“龙辰辰”玩具每件售价均为$80$元,且全部售完,求两次的利润总和。
(1)求第一次购进的“龙辰辰”玩具每件的进价;
(2)若两次购进的“龙辰辰”玩具每件售价均为$80$元,且全部售完,求两次的利润总和。
答案:
22. 解:
(1)设第一次购进的“龙辰辰”玩具每件的进价为$x$元,则第二次购进的“龙辰辰”玩具每件的进价为$1.2x$元。依题意,得$\frac{3000}{x} - \frac{3000}{1.2x} = 10$,解得$x = 50$,经检验,$x = 50$是原分式方程的解,所以第一次购进的“龙辰辰”玩具每件的进价为 50 元;
(2)由题意知,第二次购进的“龙辰辰”玩具每件的进价为 60 元,因为$\frac{3000}{50}×(80 - 50) + \frac{3000}{60}×(80 - 60) = 2800$(元),所以两次利润总和为 2800 元。
(1)设第一次购进的“龙辰辰”玩具每件的进价为$x$元,则第二次购进的“龙辰辰”玩具每件的进价为$1.2x$元。依题意,得$\frac{3000}{x} - \frac{3000}{1.2x} = 10$,解得$x = 50$,经检验,$x = 50$是原分式方程的解,所以第一次购进的“龙辰辰”玩具每件的进价为 50 元;
(2)由题意知,第二次购进的“龙辰辰”玩具每件的进价为 60 元,因为$\frac{3000}{50}×(80 - 50) + \frac{3000}{60}×(80 - 60) = 2800$(元),所以两次利润总和为 2800 元。
23. 一个长方形的长、宽分别为$a(cm)$、$b(cm)$,如果将长方形的长和宽分别增加$2cm$和$3cm$。
(1)新长方形的面积比原长方形的面积增加了
(2)若$a = 4cm$,$b = 3cm$,求长方形增加的面积
(3)如果新长方形的面积是原长方形面积的$2$倍,求$(a - 2)(b - 3)$的值
(1)新长方形的面积比原长方形的面积增加了
$(3a + 2b + 6)\text{cm}^2$
;(2)若$a = 4cm$,$b = 3cm$,求长方形增加的面积
$24\text{cm}^2$
;(3)如果新长方形的面积是原长方形面积的$2$倍,求$(a - 2)(b - 3)$的值
$12$
。
答案:
23. 解:
(1)由题意,得$(a + 2)(b + 3) - ab = ab + 3a + 2b + 6 - ab = (3a + 2b + 6)\text{cm}^2$;
(2)当$a = 4\text{cm}$,$b = 3\text{cm}$时,长方形增加的面积为$3a + 2b + 6 = 3×4 + 2×3 + 6 = 12 + 6 + 6 = 24(\text{cm}^2)$;
(3)因为$(a + 2)(b + 3) = 2ab$,所以$ab + 3a + 2b + 6 = 2ab$,所以$ab - 3a - 2b + 6 = 12$,$ab - 2b - 3a + 6 = 12$,$b(a - 2) - 3(a - 2) = 12$,所以$(a - 2)(b - 3) = 12$。
(1)由题意,得$(a + 2)(b + 3) - ab = ab + 3a + 2b + 6 - ab = (3a + 2b + 6)\text{cm}^2$;
(2)当$a = 4\text{cm}$,$b = 3\text{cm}$时,长方形增加的面积为$3a + 2b + 6 = 3×4 + 2×3 + 6 = 12 + 6 + 6 = 24(\text{cm}^2)$;
(3)因为$(a + 2)(b + 3) = 2ab$,所以$ab + 3a + 2b + 6 = 2ab$,所以$ab - 3a - 2b + 6 = 12$,$ab - 2b - 3a + 6 = 12$,$b(a - 2) - 3(a - 2) = 12$,所以$(a - 2)(b - 3) = 12$。
查看更多完整答案,请扫码查看


