《2025年暑假衔接起跑线七升八数学浙教版》

10. 如图，一根旗杆在离地面$9m$处的点$C$断裂，旗杆顶部落在离旗杆底部$12m$处。问：旗杆折断之前有多高?

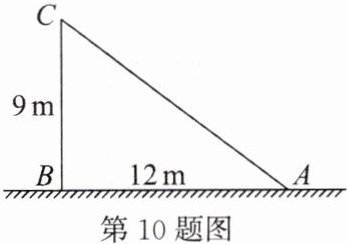
解: 在 $ \mathrm { Rt } \triangle A B C $ 中, 因为 $ \angle B = 90 ^ { \circ } $, 所以 $ A C = \sqrt { A B ^ { 2 } + B C ^ { 2 } } = \sqrt { 9 ^ { 2 } + 12 ^ { 2 } } = 15 ( \mathrm { m } ) $, 所以旗杆的长 $ = 9 + 15 = $24$( \mathrm { m } ) $。

答案： 解: 在 $ \mathrm { Rt } \triangle A B C $ 中, 因为 $ \angle B = 90 ^ { \circ } $, 所以 $ A C = \sqrt { A B ^ { 2 } + B C ^ { 2 } } = \sqrt { 9 ^ { 2 } + 12 ^ { 2 } } = 15 ( \mathrm { cm } ) $, 所以旗杆的长 $ = 9 + 15 = 24 ( \mathrm { m } ) $。

11. 如图，在四边形$ABCD$中，$AB=AD=8$，$\angle A=60^{\circ}$，$\angle D=150^{\circ}$，四边形$ABCD$的周长为32，求$BC$和$CD$的长度。

$BC=$10，$CD=$6。

答案： 解: 连结 $ B D $。因为 $ A B = A D, \angle A = 60 ^ { \circ } $, 所以 $ \triangle A B D $ 是等边三角形, 所以 $ B D = A B = 8, \angle A D B = 60 ^ { \circ } $。因为 $ \angle A D C = 150 ^ { \circ } $, 所以 $ \angle B D C = 90 ^ { \circ } $, 所以 $ \triangle B C D $ 是直角三角形。因为四边形 $ A B C D $ 的周长为 32, $ A B = A D = 8 $, 所以 $ B C + C D = 16 $。设 $ C D = x $, 则 $ B C = 16 - x $。在 $ \mathrm { Rt } \triangle B C D $ 中, $ B C ^ { 2 } = C D ^ { 2 } + B D ^ { 2 } $, 所以 $ ( 16 - x ) ^ { 2 } = x ^ { 2 } + 8 ^ { 2 } $, 解得 $ x = 6 $, 则 $ 16 - x = 10 $。故 $ C D = 6, B C = 10 $。

12. 如图，有一张直角三角形纸片，两直角边$AC=6cm$，$BC=8cm$，将$\triangle ABC$折叠，使点$B$与点$A$重合，折痕为$DE$，求$CD$的长。

解: 设 $ C D = x $, 则 $ A D = B D = 8 - x $。在 $ \mathrm { Rt } \triangle A C D $ 中, $ A D ^ { 2 } = A C ^ { 2 } + C D ^ { 2 } $, 即 $ ( 8 - x ) ^ { 2 } = 6 ^ { 2 } + x ^ { 2 } $, 解得 $ x = $$\frac { 7 } { 4 }$, 即 $ C D $ 的长为$\frac { 7 } { 4 }$$\mathrm { cm } $。

答案： 解: 设 $ C D = x $, 则 $ A D = B D = 8 - x $。在 $ \mathrm { Rt } \triangle A C D $ 中, $ A D ^ { 2 } = A C ^ { 2 } + C D ^ { 2 } $, 即 $ ( 8 - x ) ^ { 2 } = 6 ^ { 2 } + x ^ { 2 } $, 解得 $ x = \frac { 7 } { 4 } $, 即 $ C D $ 的长为 $ \frac { 7 } { 4 } \mathrm { cm } $。

13. 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小明以灵感，他惊喜的发现，当四个全等的直角三角形如图摆放时，可以用“面积法”来证明$a^{2}+b^{2}=c^{2}$。请你写出证明过程。

证明: 因为 $ S _ { \text { 五边形 } A B C D E } = S _ { \text { 梯形 } A B F E } + S _ { \text { 梯形 } C D E F } = S _ { \text { 正方形 } A E D H } + 2 S _ { \text { 直角三角形 } } $, 即 $ \frac { 1 } { 2 } ( b + a + b ) \cdot b + \frac { 1 } { 2 } ( a + a + b ) \cdot a = c ^ { 2 } + 2 × \frac { 1 } { 2 } a b $, 即 $ \frac { 1 } { 2 } a b + b ^ { 2 } + a ^ { 2 } + \frac { 1 } { 2 } a b = c ^ { 2 } + a b $, 即 $ a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $。

答案： 证明: 因为 $ S _ { \text { 五边形 } A B C D E } = S _ { \text { 梯形 } A B F E } + S _ { \text { 梯形 } C D E F } = S _ { \text { 正方形 } A E D H } + 2 S _ { \text { 直角三角形 } } $, 即 $ \frac { 1 } { 2 } ( b + a + b ) \cdot b + \frac { 1 } { 2 } ( a + a + b ) \cdot a = c ^ { 2 } + 2 \times \frac { 1 } { 2 } a b $, 即 $ \frac { 1 } { 2 } a b + b ^ { 2 } + a ^ { 2 } + \frac { 1 } { 2 } a b = c ^ { 2 } + a b $, 即 $ a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $。