第168页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
问题探究
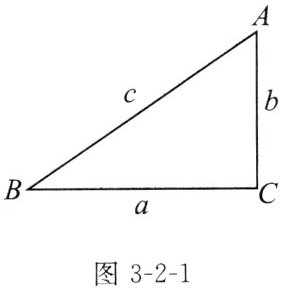
如图3-2-1,△ABC的三边a,b,c满足$a^{2}+b^{2}= c^{2}$,能否证明△ABC为直角三角形?
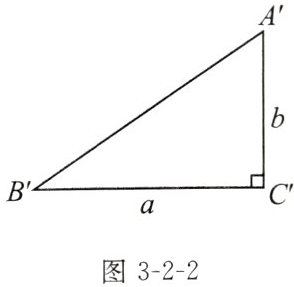
我们先作一个Rt△A'B'C',使∠C'= 90°,B'C'=
根据勾股定理,得A'B'^2=
因为AB^2= a^2+b^2,
所以A'B'= AB。
根据“
于是∠C= ∠C'=
如图3-2-1,△ABC的三边a,b,c满足$a^{2}+b^{2}= c^{2}$,能否证明△ABC为直角三角形?


我们先作一个Rt△A'B'C',使∠C'= 90°,B'C'=
a
,A'C'= b(图3-2-2),再设法证明△A'B'C'与△ABC全等。根据勾股定理,得A'B'^2=
$a^{2}$
+b^2。因为AB^2= a^2+b^2,
所以A'B'= AB。
根据“
SSS
”,可知△ABC≌△A'B'C'。于是∠C= ∠C'=
90
°,即△ABC是直角三角形。
答案:
a $a^{2}$ SSS 90
例1 下列几组数中,不能作为一个直角三角形的三边长的是(
A.1.5,2,2.5
B.3,4,5
$C.3^2,4^2,5^2$
D.30,40,50
C
)A.1.5,2,2.5
B.3,4,5
$C.3^2,4^2,5^2$
D.30,40,50
答案:
C
查看更多完整答案,请扫码查看


