《2025年全品学练考八年级数学上册苏科版江苏专版》

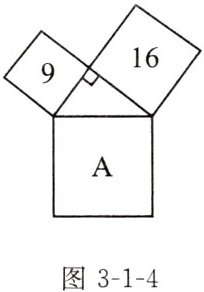
练习1 如图3-1-4,数字代表所在正方形的面积,则A所代表的正方形的面积为25.

答案： 25

练习2 如图3-1-5,在四边形ABCD中,∠DAB= ∠BCD= 90°,分别以四边形ABCD的四条边为一边向外作正方形,面积分别为a,b,c,d.若b+c= 12,则a+d= 12.

答案： 12

练习3 如图3-1-6,△ABC中,∠ACB= 90°,分别以AC,AB为边向外作正方形,面积分别为$S_{1},S_{2},$若$S_{1}= 2,S_{2}= 5,$则BC= $\sqrt{3}$.

答案： $ \sqrt{3} $

例1(教材典题)如图3-1-7,已知直角三角形的两边长,求第三边的长.

答案： 解:
(1)根据勾股定理,得$ 12^2+5^2=c^2 $,即$ c^2=169 $.所以$ c=\sqrt{169}=13 $.
(2)根据勾股定理,得$ 2^2+b^2=5^2 $,即$ b^2=21 $.所以$ b=\sqrt{21} $.

例2(教材典题)在数轴上画出$\sqrt{5}$对应的点.

答案：
解:如图,画一个直角边分别为2和1的直角三角形.由勾股定理知,斜边为$ \sqrt{2^2+1^2}=\sqrt{5} $.以原点为圆心,斜边长为半径画弧,与数轴正半轴交于点P,则P为$ \sqrt{5} $对应的点.

反思
如何在数轴上表示带根号的无理数？

答案： 解:利用数轴画出以带根号的无理数为斜边的直角三角形,再借助圆规来完成.