《2025年全品学练考八年级数学上册苏科版江苏专版》

(2)如图1-3-12,已知∠1= ∠2,直接根据“ASA”判定△ABD≌△ACD,则需要补充的一个条件为∠BAD=∠CAD;

答案： ∠BAD=∠CAD

(3)如图1-3-13,点D,A,B在同一条直线上,∠CAD= ∠EAB,AE= AC,直接根据“ASA”判定△ABC≌△ADE,则需要添加的一个条件是∠C=∠E.

答案： ∠C=∠E

例 (教材典题)如图1-3-14,在△ABC中,D是BC的中点,点E,F分别在AB,AC上,且DE//AC,DF//AB.求证:△EBD≌△FDC.

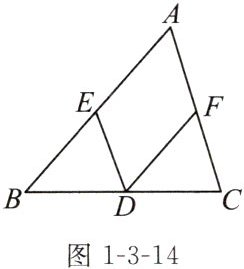
答案： 证明:
∵DE//AC,DF//AB,
∴∠EDB=∠C,∠B=∠FDC(两直线平行,同位角相等).
∵D是BC的中点,
∴BD=DC.
在△EBD和△FDC中,∠EDB=∠C，
BD=DC，
∠B=∠FDC，
∴△EBD≌△FDC(ASA).

练习 如图1-3-15,AB,CD相交于点O,O是AB的中点,AC//BD.
求证:△ACO≌△BDO.

答案： 证明:
∵O是AB的中点,
∴AO=BO.
∵AC//BD,
∴∠A=∠B.
在△ACO与△BDO中,∠A=∠B，
AO=BO，
∠AOC=∠BOD，
∴△ACO≌△BDO.

拓展 如图1-3-16,在四边形ABCD中,∠B= ∠DAB= 90°,DF⊥AC于点F,延长DF交AB于点E,AE= BC.求证:AC= DE.

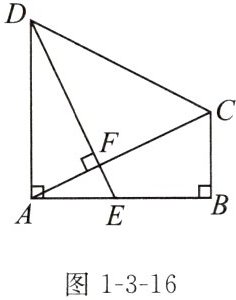
答案： 证明:
∵DF⊥AC,
∴∠AFE=90°.
∴∠CAB+∠AED=90°.
∵∠B=90°,
∴∠CAB+∠ACB=90°.
∴∠ACB=∠DEA.
在△ABC和△DAE中,∠ACB=∠DEA，
BC=AE，
∠B=∠DAE，
∴△ABC≌△DAE(ASA).
∴AC=DE.

反思用ASA证明三角形全等,如果有两个角对应相等时,怎么找第三个条件?

答案： 解：
根据三角形内角和定理$A + B + C=180^{\circ}$（$A$、$B$、$C$为三角形内角），若已知两个角对应相等，那么这两个角的夹边也必然对应相等。
所以第三个条件是这两个角的夹边对应相等。